
 與
與 滿足:|
滿足:| |=4,|
|=4,| |=3,(2
|=3,(2 +3
+3 )•(2
)•(2 -
- )=61.
)=61. •
• 的值;
的值; 與
與 的夾角;
的夾角; -
-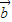 |的值.
|的值. +3
+3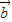 )•(2
)•(2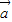 -
-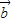 )=61得,4
)=61得,4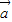 2+4
2+4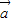 •
•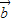 -3
-3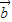 2=61將|
2=61將|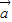 |=4,|
|=4,|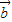 |=3,代入即可求得兩向量的內積;
|=3,代入即可求得兩向量的內積;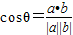 求出向量
求出向量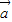 與
與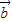 的夾角余弦,再由出對應的角;
的夾角余弦,再由出對應的角;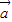 -
-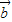 )2=
)2=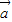 2-2
2-2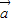 •
•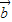 +
+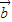 2=13,再開方求出兩向量差的模.
2=13,再開方求出兩向量差的模.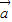 +3
+3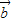 )•(2
)•(2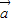 -
-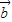 )=61得,4
)=61得,4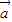 2+4
2+4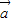 •
•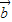 -3
-3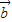 2=61.
2=61.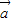 |=4,|
|=4,|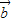 |=3,可得
|=3,可得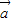 •
•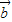 =6. …(4分)
=6. …(4分) 與
與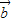 的夾角為θ,
的夾角為θ,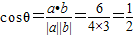 ,
,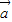 與
與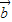 的夾角為60°. …(8分)
的夾角為60°. …(8分)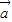 -
-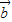 )2=
)2=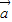 2-2
2-2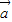 •
•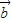 +
+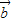 2=13可得,
2=13可得,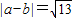 .…(12分)
.…(12分)

 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com