
某工廠2010年第三季度生產的A,B,C,D四種型號的產品產量用條形圖形表示如圖,現用分層抽樣的方法從中選取50件樣品參加2011年4月份的一個展銷會。

(1)A,B,C,D型號的產品各抽取多少件?
(2)從50件樣品隨機地抽取2件,求這2件產品恰好是不同型號產品的概率。
(3)從A,C型號的樣品中隨機地抽取3件,用ξ表示抽取A型號的產品件數,求ξ的分布列和數學期望
解:(1)從條形圖上可知,共生產產品有50+100+150+200=500(件)
樣品比為 =
=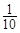 ,
,
所以A,B,C,D四種型號的產品分別取
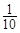 ×100=10,
×100=10,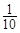 ×200=20,
×200=20,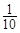 ×50=5,
×50=5,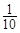 ×150=15,
×150=15,
即樣本中應抽取A產品10件,B產品20件,C產品5件,D產品15件……4分
(2)從50件產品中任取2件共有 =1225種方法,
=1225種方法,
2件恰為同一產品的方法為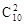 +
+ +
+ +
+ =350種,
=350種,
所以2件恰好為不同型號的產品的概率為 ………………………8分
………………………8分
(3)P(ξ=0)= , P(ξ=1)=
, P(ξ=1)= ,
,
P(ξ=2)=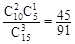 ,P(ξ=3)=
,P(ξ=3)=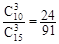 ,
,
所以ξ的分布列為
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
Eξ= +2×
+2× +3×
+3× =2………………………………………12分
=2………………………………………12分
【解析】略


科目:高中數學 來源: 題型:
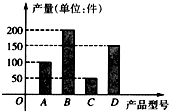 某工廠2010年第三季度生產的A,B,C,D四種型號的產品產量用條形圖形表示如圖,現用分層抽樣的方法從中選取50件樣品參加2011年4月份的一個展銷會.
某工廠2010年第三季度生產的A,B,C,D四種型號的產品產量用條形圖形表示如圖,現用分層抽樣的方法從中選取50件樣品參加2011年4月份的一個展銷會.查看答案和解析>>
科目:高中數學 來源:2010-2011學年湖北省天門市高三天5月模擬文科數學試題 題型:解答題
某工廠2010年第三季度生產的A,B,C,D四種型號的產品產量用條形圖形表示如圖,現用分層抽樣的方法從中選取50件樣品參加2011年4月份的一個展銷會。
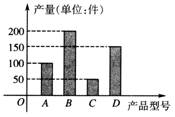
(1)A,B,C,D型號的產品各抽取多少件?
(2)從50件樣品隨機地抽取2件,求這2件產品恰好是不同型號產品的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
某工廠2010年第三季度生產的A,B,C,D四種型號的產品產量用條形圖形表示如圖,現用分層抽樣的方法從中選取50件樣品參加2011年4月份的一個展銷會。
 (1)A,B,C,D型號的產品各抽取多少件?
(1)A,B,C,D型號的產品各抽取多少件?
(2)從50件樣品隨機地抽取2件,求這2件
產品恰好是不同型號產品的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
某工廠2010年第三季度生產的A,B,C,D四種型號的產品產量用條形圖形表示如圖,現用分層抽樣的方法從中選取50件樣品參加2011年4月份的一個展銷會。
 (1)A,B,C,D型號的產品各抽取多少件?
(1)A,B,C,D型號的產品各抽取多少件?
(2)從50件樣品隨機地抽取2件,求這2件
產品恰好是不同型號產品的概率。
(3)從A,C型號的樣品中隨機地抽取3件,用
ξ表示抽取A型號的產品件數,求ξ的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com