
【題目】如圖,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,圖中圓弧所在圓的圓心為點C,半徑為 ![]() ,且點P在圖中陰影部分(包括邊界)運動.若
,且點P在圖中陰影部分(包括邊界)運動.若 ![]() =x
=x ![]() +y
+y ![]() ,其中x,y∈R,則4x﹣y的取值范圍是( )
,其中x,y∈R,則4x﹣y的取值范圍是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:以A為坐標原點,AB為x軸,DA為y軸建立平面直角坐標系則A(0,0),D(0,1),C(1,1),B(2,0) 直線BD的方程為x+2y﹣2=0,C到BD的距離d= ![]() ;
;
∴以點C為圓心,以 ![]() 為半徑的圓方程為(x﹣1)2+(y﹣1)2=
為半徑的圓方程為(x﹣1)2+(y﹣1)2= ![]() ,
,
設P(m,n)則 ![]() =(m,n),
=(m,n), ![]() =(2,0),
=(2,0), ![]() =(﹣1,1);
=(﹣1,1);
∴(m,n)=(2x﹣y,y)
∴m=2x﹣y,n=y,
∵P在圓內或圓上
∴(2x﹣y﹣1)2+(y﹣1)2≤ ![]() ,
,
設4x﹣y=t,則y=4x﹣t,代入上式整理得
80x2﹣(48t+32)x+8t2+7≤0,
設f(x)=80x2﹣(48t+32)x+8t2+7,x∈[ ![]() ,
, ![]() ],
],
則 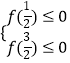 ,
,
解得2≤t≤3+ ![]() ,
,
∴4x﹣y的取值范圍是[2,3+ ![]() ].
].
故選:B.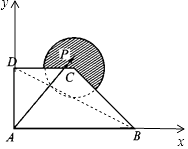


科目:高中數學 來源: 題型:
【題目】為了引導居民合理用水,某市決定全面實施階梯水價,階梯水價原則上以住宅(一套住宅為一戶)的月用水量為基準定價,具體劃分標準如表:
階梯級別 | 第一階梯水量 | 第二階梯水量 | 第三階梯水量 |
月用水量范圍(單位:立方米) | (0,10] | (10,15] | (15,+∞) |
從本市隨機抽取了10戶家庭,統計了同一個月的用水量,得到如圖所示的莖葉圖.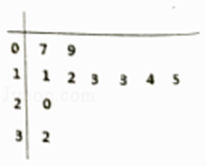
(1)現要在這10戶家庭中任意選取3戶,求取到第二階梯水量的戶數的分布列和均值;
(2)用抽到的10戶家庭作為樣本估計全市的居民用水情況,從全市依次隨機抽取10戶,若抽到n戶月用水量為第二階梯水量的可能性最大,求出n的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax3-3x2+1,若f(x)存在唯一的零點x0,且x0>0,則a的取值范圍是( )
A.(2,+∞)
B.(1,+∞)
C.(-∞,-2)
D.(-∞,-1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 (本小題滿分12分)
已知圓C:![]() ,直線
,直線![]() 過定點A (1,0).
過定點A (1,0).
(1)若![]() 與圓C相切,求
與圓C相切,求![]() 的方程;
的方程;
(2)若![]() 與圓C相交于P、Q兩點,求三角形CPQ的面積的最大值,并求此時直線
與圓C相交于P、Q兩點,求三角形CPQ的面積的最大值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 中,若對任意
中,若對任意![]() 都有
都有![]() (
(![]() 為常數)成立,則稱
為常數)成立,則稱![]() 為“等差比數列”,下面對“等差比數列” 的判斷:①
為“等差比數列”,下面對“等差比數列” 的判斷:①![]() 不可能為
不可能為![]() ;②等差數列一定是等差比數列; ③等比數列一定是等差比數列 ;④通項公式為
;②等差數列一定是等差比數列; ③等比數列一定是等差比數列 ;④通項公式為![]() (其中
(其中![]() ,且
,且![]() ,
,![]() )的數列一定是等差比數列,其中正確的判斷是( )
)的數列一定是等差比數列,其中正確的判斷是( )
A. ①③④ B. ②③④ C. ①④ D. ①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(x+1)+ax,其中a∈R.
(Ⅰ) 當a=﹣1時,求證:f(x)≤0;
(Ⅱ) 對任意x2≥ex1>0,存在x∈(﹣1,+∞),使 ![]() 成立,求a的取值范圍.(其中e是自然對數的底數,e=2.71828…)
成立,求a的取值范圍.(其中e是自然對數的底數,e=2.71828…)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com