
【題目】已知四棱錐![]() 的底面ABCD是直角梯形,AD//BC,
的底面ABCD是直角梯形,AD//BC,![]() ,
,![]() E為CD的中點(diǎn),
E為CD的中點(diǎn),![]()

(1)證明:平面PBD![]() 平面ABCD;
平面ABCD;
(2)若![]() ,PC與平面ABCD所成的角為
,PC與平面ABCD所成的角為![]() ,試問“在側(cè)面PCD內(nèi)是否存在一點(diǎn)N,使得
,試問“在側(cè)面PCD內(nèi)是否存在一點(diǎn)N,使得![]() 平面PCD?”若存在,求出點(diǎn)N到平面ABCD的距離;若不存在,請說明理由.
平面PCD?”若存在,求出點(diǎn)N到平面ABCD的距離;若不存在,請說明理由.
【答案】(1)見解析;(2)存在N點(diǎn)到平面ABCD的距離為![]()
【解析】
(1)通過證明![]() ,結(jié)合題目所給已知
,結(jié)合題目所給已知![]() ,由此證得
,由此證得![]() 平面
平面![]() ,進(jìn)而證得平面
,進(jìn)而證得平面![]() 平面
平面![]() .
.
(2)存在.通過(1)的結(jié)論,利用面面垂直的性質(zhì)定理建立空間直角坐標(biāo)系,假設(shè)存在符合題意的點(diǎn)![]() ,使
,使![]() 平面
平面![]() ,利用向量線性運(yùn)算設(shè)出
,利用向量線性運(yùn)算設(shè)出![]() 點(diǎn)坐標(biāo),結(jié)合
點(diǎn)坐標(biāo),結(jié)合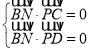 求得
求得![]() 點(diǎn)坐標(biāo),由此證得存在一點(diǎn)
點(diǎn)坐標(biāo),由此證得存在一點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() .利用點(diǎn)到平面距離的向量求法,求得點(diǎn)
.利用點(diǎn)到平面距離的向量求法,求得點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
(1)證明:由四邊形ABCD是直角梯形, AB=![]() ,BC=2AD=2,AB⊥BC,
,BC=2AD=2,AB⊥BC,
可得DC=2,∠BCD=![]() ,從而△BCD是等邊三角形,BD=2,BD平分∠ADC.
,從而△BCD是等邊三角形,BD=2,BD平分∠ADC.
∵E為CD的中點(diǎn),∴DE=AD=1,∴BD⊥AE,
又∵PB⊥AE,PB∩BD=B,∴AE⊥平面PBD.又∵AE平面ABCD∴平面PBD⊥平面ABCD.
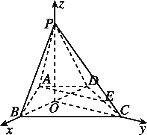
(2) 存在.在平面PBD內(nèi)作PO⊥BD于O,連接OC,又∵平面PBD⊥平面ABCD,平面PBD∩平面ABCD=BD,
∴PO⊥平面ABCD,∴∠PCO為PC與平面ABCD所成的角, 則∠PCO=
∴易得OP=OC=![]() ,PB=PD,PO⊥BD,所以O為BD的中點(diǎn),OC⊥BD.
,PB=PD,PO⊥BD,所以O為BD的中點(diǎn),OC⊥BD.
以OB,OC,OP所在的直線分別為x,y,z軸建立空間直角坐標(biāo)系,則B(1,0,0),C(0,![]() ,0)D(-1,0,0),P(0,0,
,0)D(-1,0,0),P(0,0,![]() )假設(shè)在側(cè)面
)假設(shè)在側(cè)面![]() 內(nèi)存在點(diǎn)
內(nèi)存在點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() 成立,
成立,
設(shè)![]() ,易得
,易得![]() 由
由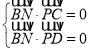 得
得![]() ,滿足題意,所以N點(diǎn)到平面ABCD的距離為
,滿足題意,所以N點(diǎn)到平面ABCD的距離為![]()


 金鑰匙試卷系列答案
金鑰匙試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
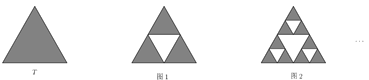
【題目】對于正三角形![]() ,挖去以三邊中點(diǎn)為頂點(diǎn)的小正三角形,得到一個新的圖形,這樣的過程稱為一次“鏤空操作“,設(shè)
,挖去以三邊中點(diǎn)為頂點(diǎn)的小正三角形,得到一個新的圖形,這樣的過程稱為一次“鏤空操作“,設(shè)![]() 是一個邊長為1的正三角形,第一次“鏤空操作”后得到圖1,對剩下的3個小正三角形各進(jìn)行一次“鏤空操作”后得到圖2,對剩下的小三角形重復(fù)進(jìn)行上述操作,設(shè)
是一個邊長為1的正三角形,第一次“鏤空操作”后得到圖1,對剩下的3個小正三角形各進(jìn)行一次“鏤空操作”后得到圖2,對剩下的小三角形重復(fù)進(jìn)行上述操作,設(shè)![]() 是第
是第![]() 次挖去的小三角形面積之和(如
次挖去的小三角形面積之和(如![]() 是第1次挖去的中間小三角形面積,
是第1次挖去的中間小三角形面積,![]() 是第2次挖去的三個小三角形面積之和),
是第2次挖去的三個小三角形面積之和),![]() 是前
是前![]() 次挖去的所有三角形的面積之和,則
次挖去的所有三角形的面積之和,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標(biāo)原點(diǎn),離心率等于
的中心在坐標(biāo)原點(diǎn),離心率等于![]() ,該橢圓的一個長軸端點(diǎn)恰好是拋物線
,該橢圓的一個長軸端點(diǎn)恰好是拋物線![]() 的焦點(diǎn).
的焦點(diǎn).
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() 與橢圓
與橢圓![]() 的兩個交點(diǎn)記為
的兩個交點(diǎn)記為![]() 、
、![]() ,其中點(diǎn)
,其中點(diǎn)![]() 在第一象限,點(diǎn)
在第一象限,點(diǎn)![]() 、
、![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側(cè)的動點(diǎn).當(dāng)
兩側(cè)的動點(diǎn).當(dāng)![]() 、
、![]() 運(yùn)動時,滿足
運(yùn)動時,滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值?若是,求出該定值;若不是,請說明理由.
的斜率是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 在區(qū)間
在區(qū)間![]() 上的最值;
上的最值;
(2)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(3)當(dāng)![]() 時,有
時,有![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中,![]() ,
,![]() ,已知G與E分別為
,已知G與E分別為![]() 和
和![]() 的中點(diǎn),D和F分別為線段AC和AB上的動點(diǎn)(不包括端點(diǎn)),若
的中點(diǎn),D和F分別為線段AC和AB上的動點(diǎn)(不包括端點(diǎn)),若![]() ,則線段DF的長度的平方取值范圍為( ).
,則線段DF的長度的平方取值范圍為( ).

A.![]() B.
B.![]() C.
C. D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(1)求函數(shù)![]() 的極值;
的極值;
(2)問:是否存在實(shí)數(shù)![]() ,使得
,使得![]() 有兩個相異零點(diǎn)?若存在,求出
有兩個相異零點(diǎn)?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】二十四節(jié)氣是中國古代的一種指導(dǎo)農(nóng)事的補(bǔ)充歷法,是我國勞動人民長期經(jīng)驗(yàn)的積累成果和智慧的結(jié)晶,被譽(yù)為“中國的第五大發(fā)明”.由于二十四節(jié)氣對古時候農(nóng)事的進(jìn)行起著非常重要的指導(dǎo)作用,所以勞動人民編寫了很多記憶節(jié)氣的歌謠:春雨驚春清谷天,夏滿芒夏暑相連,秋處露秋寒霜降,冬雪雪冬小大寒.《易經(jīng)》里對二十四節(jié)氣的晷影長的記錄中,冬至和夏至的晷影長是實(shí)測得到的,其他節(jié)氣的晷影是按照等差數(shù)列的規(guī)律計(jì)算出來的,在下表中,冬至的晷影最長為130.0寸,夏至的晷影最短為14.8寸,那么《易經(jīng)》中所記錄的清明的晷影長應(yīng)為( )

A.77.2寸B.72.4寸C.67.3寸D.62.8寸
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .(其中
.(其中![]() 為自然對數(shù)的底數(shù))
為自然對數(shù)的底數(shù))
(1)若![]() ,且
,且![]() 在
在![]()
![]() 上是增函數(shù),求
上是增函數(shù),求![]() 的最小值;
的最小值;
(2)設(shè)![]() ,若對任意
,若對任意![]() 、
、![]() 恒有
恒有![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
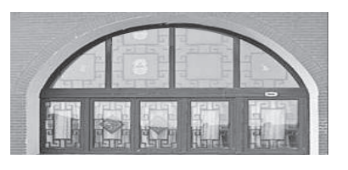
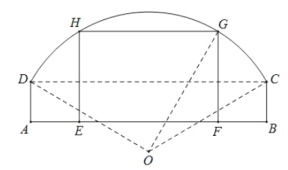
【題目】如下圖所示,某窯洞窗口形狀上部是圓弧![]() ,下部是一個矩形
,下部是一個矩形![]() ,圓弧
,圓弧![]() 所在圓的圓心為O,經(jīng)測量
所在圓的圓心為O,經(jīng)測量![]() 米,
米,![]() 米,
米,![]() ,現(xiàn)根據(jù)需要把此窯洞窗口形狀改造為矩形
,現(xiàn)根據(jù)需要把此窯洞窗口形狀改造為矩形![]() ,其中E,F在邊
,其中E,F在邊![]() 上,G,H在圓弧
上,G,H在圓弧![]() 上.設(shè)
上.設(shè)![]() ,矩形
,矩形![]() 的面積為S.
的面積為S.
(1)求矩形![]() 的面積S關(guān)于變量
的面積S關(guān)于變量![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)求![]() 為何值時,矩形
為何值時,矩形![]() 的面積S最大?
的面積S最大?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com