
【題目】已知橢圓![]() (
(![]() )的離心率為
)的離心率為![]() ,以
,以![]() 的短軸為直徑的圓與直線
的短軸為直徑的圓與直線![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() .已知
.已知![]() 上存在點
上存在點![]() ,使得
,使得![]() 是以
是以![]() 為頂角的等腰直角三角形,若
為頂角的等腰直角三角形,若![]() 在直線
在直線![]() 的右下方,求
的右下方,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由![]() 的短軸為直徑的圓與直線
的短軸為直徑的圓與直線![]() 相切求出
相切求出![]() ,再由離心率和
,再由離心率和![]() 關系,可求出橢圓標準方程;
關系,可求出橢圓標準方程;
(2)將直線![]() 與橢圓方程聯立,消元整理,由根與系數關系,得到
與橢圓方程聯立,消元整理,由根與系數關系,得到![]() 的兩個關系式,再從已知條件尋找
的兩個關系式,再從已知條件尋找![]() 第三個等量關系,根據已知結合平面圖形,可得
第三個等量關系,根據已知結合平面圖形,可得![]() 軸,過
軸,過![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,則
,則![]() 為線段
為線段![]() 的中點,得
的中點,得![]() ,進而有
,進而有![]() ,代入直線
,代入直線![]() 方程,得到
方程,得到![]() 等量關系,求解關于
等量關系,求解關于![]() 方程組,即可求出
方程組,即可求出![]() .
.
(1)依題意,![]() ,
,
因為離心率![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以![]() 的標準方程為
的標準方程為![]() .
.
(2)因為直線![]() 的傾斜角為
的傾斜角為![]() ,
,
且![]() 是以
是以![]() 為頂角的等腰直角三角形,
為頂角的等腰直角三角形,
![]() 在直線
在直線![]() 的右下方,所以
的右下方,所以![]() 軸,
軸,
過![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,則
,則![]() 為線段
為線段![]() 的中點,
的中點,
所以![]() ,故
,故![]() ,
,
所以![]() ,即
,即![]() ,
,
整理得![]() .①
.①
由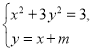 得
得![]() .
.
所以![]() ,解得
,解得![]() ,
,
所以![]() ,②
,②
![]() ,③
,③
由①![]() ②得,
②得,![]() ,④
,④
將④代入②得![]() ,⑤
,⑤
將④⑤代入③得![]() ,解得
,解得![]() .
.
綜上,![]() 的值為
的值為![]() .
.



科目:高中數學 來源: 題型:
【題目】如果無窮數列{an}的所有項恰好構成全體正整數的一個排列,則稱數列{an}具有性質P.
(Ⅰ)若an![]() (k∈N*),判斷數列{an}是否具有性質P,并說明理由,
(k∈N*),判斷數列{an}是否具有性質P,并說明理由,
(Ⅱ)若數列{an}具有性質P,求證:{an}中一定存在三項ai,aj,ak(i<j<k)構成公差為奇數的等差數列;
(Ⅲ)若數列{an}具有性質P,則{an}中是否一定存在四項ai,aj,ak,al,(i<j<k<l)構成公差為奇數的等差數列?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:給定整數i,如果非空集合滿足如下3個條件:
①![]() ;②
;②![]() ;③
;③![]() ,若
,若![]() ,則
,則![]() .
.
則稱集合A為“減i集”
(1)![]() 是否為“減0集”?是否為“減1集”?
是否為“減0集”?是否為“減1集”?
(2)證明:不存在“減2集”;
(3)是否存在“減1集”?如果存在,求出所有“減1集”;如果不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
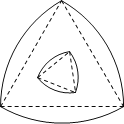
【題目】勒洛三角形是具有類似圓的“定寬性”的曲線,它是由德國機械工程專家、機構運動學家勒洛首先發現,其作法是:以等邊三角形每個頂點為圓心,以邊長為半徑,在另兩個頂點間作一段弧,三段弧圍成的曲邊三角形就是勒洛三角形.如圖中的兩個勒洛三角形,它們所對應的等邊三角形的邊長比為![]() ,若從大的勒洛三角形中隨機取一點,則此點取自小勒洛三角形內的概率為______.
,若從大的勒洛三角形中隨機取一點,則此點取自小勒洛三角形內的概率為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,且橢圓上存在一點
,且橢圓上存在一點![]() ,滿足
,滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 右焦點
右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 的內切圓的半徑的最大值.
的內切圓的半徑的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() (
(![]() )的離心率是
)的離心率是![]() ,點
,點![]() 在短軸
在短軸![]() 上,且
上,且![]() 。
。
(1)球橢圓![]() 的方程;
的方程;
(2)設![]() 為坐標原點,過點
為坐標原點,過點![]() 的動直線與橢圓交于
的動直線與橢圓交于![]() 兩點。是否存在常數
兩點。是否存在常數![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com