
【題目】己知⊙O:x2+y2=6,P為⊙O上動點,過P作PM⊥x軸于M,N為PM上一點,且 ![]() . (Ⅰ)求點N的軌跡C的方程;
. (Ⅰ)求點N的軌跡C的方程;
(Ⅱ)若A(2,1),B(3,0),過B的直線與曲線C相交于D、E兩點,則kAD+kAE是否為定值?若是,求出該值;若不是,說明理由.
【答案】解:(Ⅰ)設N(x,y),P(x0 , y0),則M(x0 , 0), ![]() ,
, ![]()
由 ![]() ,得
,得  ,
,
∴ 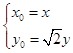
由于點P在圓O:x2+y2=6上,則有 ![]() ,即
,即 ![]() .
.
∴點N的軌跡C的方程為 ![]() .
.
(Ⅱ) 設D(x1 , y1),E(x2 , y2),過點B的直線DE的方程為y=k(x﹣3),
由 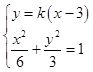 消去y得:(2k2+1)x2﹣12k2x+18k2﹣6=0,其中△>0
消去y得:(2k2+1)x2﹣12k2x+18k2﹣6=0,其中△>0
∴ ![]() ;
;
∴ ![]()
= 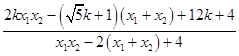
= 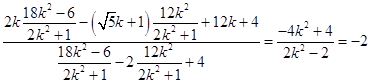
∴kAD+kAE是定值﹣2.
【解析】(Ⅰ)設M(x,y),則可設P(x,y0),Q(x,0),根據又 ![]() ,可確定y0=3y,進而可知點P的坐標代入圓的方程,求得曲線C的方程.(Ⅱ)設D(x1 , y1),E(x2 , y2),設出過點B的直線DE的方程,與題意方程聯立,利用韋達定理求出橫坐標的和與乘積,求出kAD+kAE化簡即可判斷否為定值.
,可確定y0=3y,進而可知點P的坐標代入圓的方程,求得曲線C的方程.(Ⅱ)設D(x1 , y1),E(x2 , y2),設出過點B的直線DE的方程,與題意方程聯立,利用韋達定理求出橫坐標的和與乘積,求出kAD+kAE化簡即可判斷否為定值.


科目:高中數學 來源: 題型:
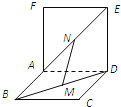
【題目】如圖,兩個正方形ABCD和ADEF所在平面互相垂直,設M、N分別是BD和AE的中點,那么![]() ;
;![]() 面CDE;
面CDE;![]() ;
;![]() MN,CE異面其中正確結論的序號是______.
MN,CE異面其中正確結論的序號是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐S﹣ABC中,側面SAB與側面SAC均為等邊三角形,∠BAC=90°,O為BC中點. (Ⅰ)證明:SO⊥平面ABC;
(Ⅱ)求二面角A﹣SC﹣B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() ,直線
,直線![]() :
:![]() .
.
(1)若直線![]() 被圓
被圓![]() 截得的弦長為
截得的弦長為![]() ,求實數
,求實數![]() 的值;
的值;
(2)當![]() 時,由直線
時,由直線![]() 上的動點
上的動點![]() 引圓
引圓![]() 的兩條切線,若切點分別為
的兩條切線,若切點分別為![]() ,
,![]() ,則在直線
,則在直線![]() 上是否存在一個定點?若存在,求出該定點的坐標;若不存在,請說明理由.
上是否存在一個定點?若存在,求出該定點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一臺機器按不同的轉速生產出來的某機械零件有一些會有缺點,每小時生產有缺點零件的多少,隨機器的運轉的速度而變化,具有線性相關關系,下表為抽樣試驗的結果:
轉速 | 8 | 10 | 12 | 14 | 16 |
每小時生產有缺點的零件數 | 5 | 7 | 8 | 9 | 11 |
(1)如果![]() 對
對![]() 有線性相關關系,求回歸方程;
有線性相關關系,求回歸方程;
(2)若實際生產中,允許每小時生產的產品中有缺點的零件最多有1個,那么機器的運轉速度應控制在什么范圍內?參考公式:![]() ,
,
 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了分析本校高中生的性別與是否喜歡數學之間的關系,在高中生中隨機地抽取了90名學生調查,得到了如下列聯表:
喜歡數學 | 不喜歡數學 | 總計 | |
男 | 30 | ① | 45 |
女 | ② | 25 | 45 |
總計 | ③ | ④ | 90 |
(1)求①②③④處分別對應的值;
(2)能有多大把握認為“高中生的性別與喜歡數學”有關?
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com