
設(shè)a、b是不相等的實(shí)數(shù),試探求證明不等式(a4+b4)(a2+b2)>(a3+b3)2的方法.
探究思路:對(duì)于不等式的證明比較常見(jiàn)的方法是作差法,即求出不等式兩邊式子的差,再根據(jù)差與零的關(guān)系來(lái)達(dá)到證明不等式的目的.現(xiàn)在我們又學(xué)習(xí)了向量數(shù)量積的坐標(biāo)表示,因此可以根據(jù)不等式結(jié)構(gòu)構(gòu)造向量利用向量知識(shí)來(lái)達(dá)到證明不等式的目的.
方法一:(a4+b4)(a2+b2)-(a3+b3)2
=a6+b6+a4b2+a2b4-a6-b6-2a3b3
=a4b2+a2b4-2a3b3
=a2b2(a2-ab)+a2b2(b2-ab)
=a2b2(a-b)2.
由于a、b是不相等的實(shí)數(shù),則(a4+b4)(a2+b2)-(a3+b3)2=a2b2(a-b)2>0,
即(a4+b4)(a2+b2)>(a3+b3)2.
方法二:設(shè)m=(a2,b2),n=(a,b),
則m·n=a3+b3,
又a、b是不相等的實(shí)數(shù),則a2b-ab2≠0,
即向量m、n不共線(xiàn),所以有|m·n|<|m||n|,即(a4+b4)(a2+b2)>(a3+b3)2.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2004全國(guó)各省市高考模擬試題匯編(天利38套)·數(shù)學(xué) 題型:044
二次函數(shù)f(x)=ax2+bx+c(a、b、c∈R,a≠0).
(Ⅰ)對(duì)于x1、x2∈R,且x1<x2,f(x1)≠f(x2),求證:方程f(x)=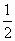 [f(x1)+f(x2)]有不相等的兩實(shí)根,且必有一根屬于(x1、x2);
[f(x1)+f(x2)]有不相等的兩實(shí)根,且必有一根屬于(x1、x2);
(Ⅱ)若方程f(x)=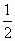 [f(x1)+f(x2)]在(x1、x2)內(nèi)的實(shí)根為m,且x1、m-
[f(x1)+f(x2)]在(x1、x2)內(nèi)的實(shí)根為m,且x1、m-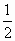 、x2成等差數(shù)列,設(shè)x=x0是f(x)的對(duì)稱(chēng)軸方程.
、x2成等差數(shù)列,設(shè)x=x0是f(x)的對(duì)稱(chēng)軸方程.
求證:x0<m2;
(Ⅲ)若a>0,f(0)=1,方程f(x)=x的兩實(shí)根為α、β,當(dāng)|β|<2,
|α-β|=2時(shí),求b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:成功之路·突破重點(diǎn)線(xiàn)·數(shù)學(xué)(學(xué)生用書(shū)) 題型:044
二次函數(shù)f(x)=ax2+bx+c(a、b、c∈R,a≠0).
(Ⅰ)對(duì)于x1、x2∈R,且x1<x2,f(x1)≠f(x2),求證:方程f(x)=![]() [f(x1)+f(x2)]有不相等的兩實(shí)根,且必有一根屬于(x1、x2);
[f(x1)+f(x2)]有不相等的兩實(shí)根,且必有一根屬于(x1、x2);
(Ⅱ)若方程f(x)=![]() [f(x1)+f(x2)]在(x1、x2)內(nèi)的實(shí)根為m,且x1、m-
[f(x1)+f(x2)]在(x1、x2)內(nèi)的實(shí)根為m,且x1、m-![]() 、x2成等差數(shù)列,設(shè)x=x0是f(x)的對(duì)稱(chēng)軸方程.求證:x0<m2.
、x2成等差數(shù)列,設(shè)x=x0是f(x)的對(duì)稱(chēng)軸方程.求證:x0<m2.
(Ⅲ)若a>0,f(0)=1,方程f(x)=x的兩實(shí)根為α、β,當(dāng)|β|<2,|α-β|=2時(shí),求b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
A.|x1|>2且|x2|>2 B.|x1+x2|>4
C.|x1+x2|<4 D.|x1|=4且|x2|=1
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
A.|x1|>2且|x2|>2 B.|x1+x2|>4
C.|x1+x2|<4 D.|x1|=4且|x2|=1
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2013屆安徽省高二下學(xué)期期中考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
已知a、b、c是互不相等的非零實(shí)數(shù).若用反證法證明三個(gè)方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一個(gè)方程有兩個(gè)相異實(shí)根.
【解析】本試題主要考查了二次方程根的問(wèn)題的綜合運(yùn)用。運(yùn)用反證法思想進(jìn)行證明。
先反設(shè),然后推理論證,最后退出矛盾。證明:假設(shè)三個(gè)方程中都沒(méi)有兩個(gè)相異實(shí)根,
則Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0.顯然不成立。
證明:假設(shè)三個(gè)方程中都沒(méi)有兩個(gè)相異實(shí)根,
則Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0.
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0. ①
由題意a、b、c互不相等,∴①式不能成立.
∴假設(shè)不成立,即三個(gè)方程中至少有一個(gè)方程有兩個(gè)相異實(shí)根.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com