
【題目】設函數f(x)=﹣x3+ax2+bx+c的導數f'(x)滿足f'(﹣1)=0,f'(2)=9.
(1)求f(x)的單調區間;
(2)f(x)在區間[﹣2,2]上的最大值為20,求c的值.
(3)若函數f(x)的圖象與x軸有三個交點,求c的范圍.
【答案】
(1)解:函數的導數f′(x)=﹣3x2+2ax+b,
∵f'(x)滿足f'(﹣1)=0,f'(2)=9,
∴ ![]() 得a=3,b=9,
得a=3,b=9,
則f(x)=﹣x3+3x2+9x+c,f′(x)=﹣3x2+6x+9=﹣3(x2﹣2x﹣3),
由f′(x)>0得﹣3(x2﹣2x﹣3)>0得x2﹣2x﹣3<0,得﹣1<x<3,
此時函數單調遞增,即遞增區間為(﹣1,3),
由f′(x)<0得﹣3(x2﹣2x﹣3)<0得x2﹣2x﹣3>0,得x<﹣1或x>3,
此時函數單調遞減,即遞減區間為(﹣∞,﹣1),(3,+∞);
(2)解:由(1)知,當x=﹣1時,函數取得極小值f(﹣1)=1+3﹣9+c=c﹣5,
f(﹣2)=8+12﹣18+c=2+c,f(2)=﹣8+12+18+c=22+c,
則f(x)在區間[﹣2,2]上的最大值為f(2)=22+c=20,
則c=﹣2.
(3)解:由(1)知當x=﹣1時,函數取得極小值f(﹣1)=1+3﹣9+c=c﹣5,
當x=3時,函數取得極大值f(3)=﹣27+27+27+c=27+c,
若函數f(x)的圖象與x軸有三個交點,
則 ![]() 得
得 ![]() ,得﹣27<c<5,
,得﹣27<c<5,
即c的范圍是(﹣27,5).
【解析】(1)求函數的導數,根據條件建立方程組關系求出a,b的值,結合函數單調性和導數之間的關系即可求f(x)的單調區間;(2)求出函數f(x)在區間[﹣2,2]上的最大值,建立方程關系即可求c的值.(3)若函數f(x)的圖象與x軸有三個交點,則等價為函數的極大值大于0,極小值小于0,解不等式即可求c的范圍.
【考點精析】解答此題的關鍵在于理解基本求導法則的相關知識,掌握若兩個函數可導,則它們和、差、積、商必可導;若兩個函數均不可導,則它們的和、差、積、商不一定不可導,以及對函數的最大(小)值與導數的理解,了解求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:
【題目】“斐波那契數列”是數學史上一個著名數列,在斐波那契數列{an}中,a1=1,a2=1,an+2=an+1+an(n∈N*)則a8=;若a2018=m2+1,則數列{an}的前2016項和是 . (用m表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數g(x)=mx2﹣2mx+n+1(m>0)在區間[0,3]上有最大值4,最小值0.
(1)求函數g(x)的解析式;
(2)設f(x)= ![]() .若f(2x)﹣k2x≤0在x∈[﹣3,3]時恒成立,求k的取值范圍.
.若f(2x)﹣k2x≤0在x∈[﹣3,3]時恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,已知長方形ABCD中,AB=2,AD=1,E為DC的中點.將△ADE沿AE折起,使得平面ADE⊥平面ABCE. 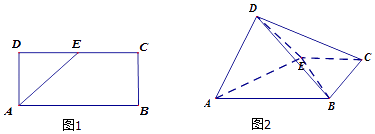
(1)求證:平面BDE⊥平面ADE
(2)求三棱錐 C﹣BDE的體積
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax3+bx2+cx在點x0處取得極大值5,其導函數y=f′(x)的圖象經過點(1,0),(2,0),如圖所示.求: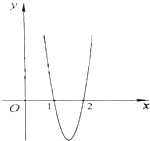
(1)x0的值;
(2)a,b,c的值.
(3)若曲線y=f(x)(0≤x≤2)與y=m有兩個不同的交點,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com