
設關于x的函數y=2cos2x﹣2acosx﹣(2a+1)的最小值為f(a),試確定滿足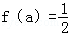 的a的值,并對此時的a值求y的最大值.
的a的值,并對此時的a值求y的最大值.
 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:解答題
已知函數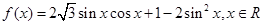 .
.
(1)求函數 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
(2)將函數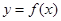 的圖像上各點的縱坐標保持不變,橫坐標縮短到原來的
的圖像上各點的縱坐標保持不變,橫坐標縮短到原來的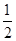 ,把所得到的圖像再向左平移
,把所得到的圖像再向左平移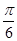 單位,得到的函數
單位,得到的函數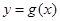 的圖像,求函數
的圖像,求函數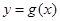 在區間
在區間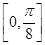 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
把函數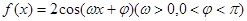 的圖像上的每一點的橫坐標伸長為原來的2倍,縱坐標不變,然后再向左平移
的圖像上的每一點的橫坐標伸長為原來的2倍,縱坐標不變,然后再向左平移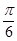 個單位后得到一個最小正周期為
個單位后得到一個最小正周期為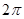 的奇函數
的奇函數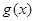 。
。
(1)求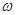 和
和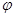 的值
的值
(2)求函數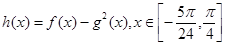 的最大值與最小值。
的最大值與最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知向量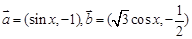 ,函數
,函數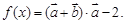
(1)求函數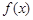 的最小正周期T及單調減區間;
的最小正周期T及單調減區間;
(2)已知a,b,c分別為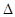 ABC內角A,B,C的對邊,其中A為銳角,
ABC內角A,B,C的對邊,其中A為銳角,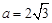 ,
,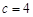 ,且
,且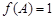 .求A,b的長和
.求A,b的長和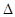 ABC的面積.
ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖所示,在 △ABC內有一內接正方形,它的一條邊在斜邊BC上,設AB=
△ABC內有一內接正方形,它的一條邊在斜邊BC上,設AB= ,∠ABC
,∠ABC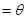

(1)求△ABC的面積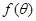 與正方形面積
與正方形面積 ;
;
(2)當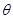 變化時,求
變化時,求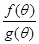 的最小值,并求出對應
的最小值,并求出對應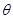 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題共9分)
已知函數f(x)=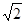 sin(2x+
sin(2x+ ),x∈R.
),x∈R.
(Ⅰ)求函數f(x)的最小正周期;
(Ⅱ)求函數f(x)在區間[- ,
, ]上的最大值和最小值。
]上的最大值和最小值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com