
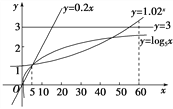
【題目】某學校為了實現(xiàn)60萬元的生源利潤目標,準備制定一個激勵招生人員的獎勵方案:在生源利潤達到5萬元時,按生源利潤進行獎勵,且資金y(單位:萬元)隨生源利潤x(單位:萬元)的增加而增加,但資金總數(shù)不超過3萬元,同時獎金不超過利潤的20%.現(xiàn)有三個獎勵模型:y=0.2x,y=log5x,y=1.02x,其中哪個模型符合該校的要求?
【答案】![]()
【解析】試題分析:資金y(單位:萬元)隨生源利潤x(單位:萬元)的增加而增加,所以是增函數(shù),三個都滿足,資金總數(shù)不超過3萬元,同時獎金不超過利潤的20%,說明![]() 且
且![]() ,所以畫出三個圖像,可得對數(shù)函數(shù)模型符合。
,所以畫出三個圖像,可得對數(shù)函數(shù)模型符合。
試題解析;借助工具作出函數(shù)y=3,y=0.2x,y=log5x,y=1.02x的圖象(如圖所示).觀察圖象可知,在區(qū)間[5,60]上,y=0.2x,y=1.02x的圖象都有一部分在直線y=3的上方,只有y=log5x的圖象始終在y=3和y=0.2x的下方,這說明只有按模型y=log5x進行獎勵才符合學校的要求.


科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]()
![]() .
.
(1)討論函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的單調性;
上的單調性;
(2)若曲線![]() 僅在兩個不同的點
僅在兩個不同的點![]() ,
,![]() 處的切線都經過點
處的切線都經過點![]() ,其中
,其中![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示是某企業(yè)2010年至2016年污水凈化量(單位: 噸)的折線圖.
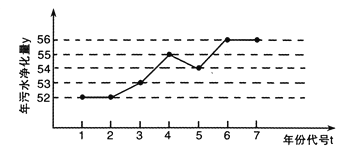
注: 年份代碼1-7分別對應年份2010-2016.
(1)由折線圖看出,可用線性回歸模型擬合![]() 和
和![]() 的關系,請用相關系數(shù)加以說明;
的關系,請用相關系數(shù)加以說明;
(2)建立![]() 關于
關于![]() 的回歸方程,預測
的回歸方程,預測![]() 年該企業(yè)污水凈化量;
年該企業(yè)污水凈化量;
(3)請用數(shù)據(jù)說明回歸方程預報的效果.
附注: 參考數(shù)據(jù):![]() ;
;
參考公式:相關系數(shù)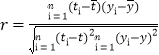 ,回歸方程
,回歸方程![]() 中斜率和截距的最小;
中斜率和截距的最小;
二乘法估汁公式分別為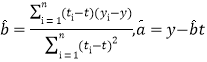 ;
;
反映回歸效果的公式為: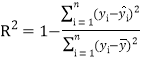 ,其中
,其中![]() 越接近于
越接近于![]() ,表示回歸的效果越好.
,表示回歸的效果越好.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,在
,在![]() 處有最小值為0.
處有最小值為0.
(1)求![]() 的值;
的值;
(2)設![]() ,
,
①求![]() 的最值及取得最值時
的最值及取得最值時![]() 的取值;
的取值;
②是否存在實數(shù)![]() ,使關于
,使關于![]() 的方程
的方程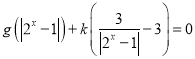 在
在![]() 上恰有一個實數(shù)解?若存在,求出實數(shù)
上恰有一個實數(shù)解?若存在,求出實數(shù)![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設![]() ,點
,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸上,且
軸上,且![]() ,
,![]() .
.
(1)當點![]() 在
在![]() 軸上運動時,求點
軸上運動時,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設點![]() 是軌跡
是軌跡![]() 上的動點,點
上的動點,點![]() 在
在![]() 軸上,圓
軸上,圓![]() 內切于
內切于![]()
![]() ,求
,求![]()
![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市需對某環(huán)城快速車道進行限速,為了調研該道路車速情況,于某個時段隨機對![]() 輛車的速度進行取樣,測量的車速制成如下條形圖:
輛車的速度進行取樣,測量的車速制成如下條形圖:
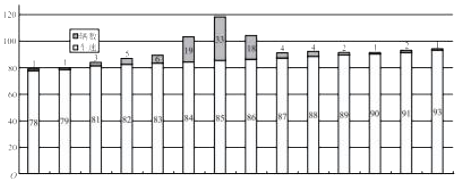
經計算:樣本的平均值![]() ,標準差
,標準差![]() ,以頻率值作為概率的估計值.已知車速過慢與過快都被認為是需矯正速度,現(xiàn)規(guī)定車速小于
,以頻率值作為概率的估計值.已知車速過慢與過快都被認為是需矯正速度,現(xiàn)規(guī)定車速小于![]() 或車速大于
或車速大于![]() 是需矯正速度.
是需矯正速度.
(1)從該快速車道上所有車輛中任取![]() 個,求該車輛是需矯正速度的概率;
個,求該車輛是需矯正速度的概率;
(2)從樣本中任取![]() 個車輛,求這
個車輛,求這![]() 個車輛均是需矯正速度的概率;
個車輛均是需矯正速度的概率;
(3)從該快速車道上所有車輛中任取![]() 個,記其中是需矯正速度的個數(shù)為
個,記其中是需矯正速度的個數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com