Question

已知函數f(x)＝的圖像在點（為自然常數）處的切線斜率為3.

(Ⅰ)求實數的值

(Ⅱ)若，且對任意的恒成立，求得最大值

(Ⅲ)當時，證明

 

Answer 1

【答案】

（1）因為f（x）=ax+xlnx，所以f'（x）=a+lnx+1．（1分）

因為函數f（x）=ax+xlnx的圖象在點x=e處的切線斜率為3，

所以f'（e）=3，即a+lne+1=3．所以a=1．（2分）

（2）解：由（1）知，f（x）=x+xlnx，

所以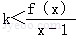對任意x＞1恒成立，即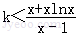對任意x＞1恒成立．（3分）

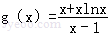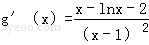令，則，（4分）

令h（x）=x﹣lnx﹣2（x＞1），則，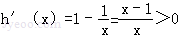

所以函數h（x）在（1，+∞）上單調遞增．（5分）

因為h（3）=1﹣ln3＜0，h（4）=2﹣2ln2＞0，

所以方程h（x）=0在（1，+∞）上存在唯一實根x₀，且滿足x₀∈（3，4）．

當1＜x＜x₀時，h（x）＜0，即g'（x）＜0，當x＞x₀時，h（x）＞0，即g'（x）＞0，

所以函數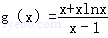在（1，x₀）上單調遞減，在（x₀，+∞）上單調遞增．

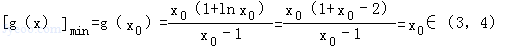．（7分）

所以k＜[g（x）]_min=x₀∈（3，4）．故整數k的最大值是3．（8分）

（3）證明：由（2）知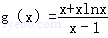，是[4，+∞）上的增函數，（9分）

所以當n＞m≥4時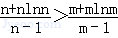，．（10分）

即n（m﹣1）（1+lnn）＞m（n﹣1）（1+lnm）．

整理，得mnlnn+mlnm＞mnlnm+nlnn+（n﹣m）．（11分）

因為n＞m，所以mnlnn+mlnm＞mnlnm+nlnn．（12分）

即lnn^mn+lnm^m＞lnm^mn+lnnⁿ．

即ln（n^mnm^m）＞ln（m^mnnⁿ）．（13分）

所以（mnⁿ）^m＞（nm^m）ⁿ．（14分）

證明2：構造函數f（x）=mxlnx+mlnm﹣mxlnm﹣xlnx，（9分）

則f'（x）=（m﹣1）lnx+m﹣1﹣mlnm．（10分）

因為x＞m≥4，所以f'（x）＞（m﹣1）lnm+m﹣1﹣mlnm=m﹣1﹣lnm＞0．

所以函數f（x）在[m，+∞）上單調遞增．（11分）

因為n＞m，所以f（n）＞f（m）．

所以mnlnn+mlnm﹣mnlnm﹣nlnn＞m²lnm+mlnm﹣m²lnm﹣mlnm=0．（12分）

即mnlnn+mlnm＞mnlnm+nlnn．

即lnn^mn+lnm^m＞lnm^mn+lnnⁿ．

即ln（n^mnm^m）＞ln（m^mnnⁿ）．（13分）

所以（mnⁿ）^m＞（nm^m）ⁿ．

【解析】略