
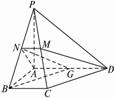
(1)求證:PB⊥DM;
(2)求CD與平面ADMN所成的角.
解法一:(1)證明:∵N是PB的中點,PA=AB,?
∴AN⊥PB.?
∵AD⊥平面PAB,∴AD⊥PB.?
從而PB⊥平面ADMN.?
∵DM ![]() 面ADMN,
面ADMN,
∴PB⊥DM.?
(2)如圖,取AD的中點C,連結BG,NG,
則BG∥CD,?

∴BG與平面ADMN所成的角和CD與平面ADMN所成的角相等.?
∵PB⊥平面ADMN,?
∴∠BGN是BG與平面ADMN所成的角.?
在Rt△BGH中,
sin∠BGN=![]() =
=![]() .?
.?
故CD與平面ADMN所成的角是arcsin![]() .
.
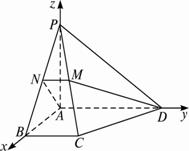
解法二:如圖,以A為坐標原點建立空間直角坐標系A—xyz,設BC=1,則A(0,0,0)?,P(0,0,2),B(2,0,0),C(2,1,0),M(1,![]() ,1),D(0,2,0).?
,1),D(0,2,0).?
(1)∵![]() ·
·![]() =(2,0,-2)·(1,-
=(2,0,-2)·(1,-![]() ,1)=0,?
,1)=0,?
∴PB⊥DM.?
(2)∵![]() ·
·![]() =(2,0,-2)·(0,2,0)=0,?
=(2,0,-2)·(0,2,0)=0,?
∴PB⊥AD,又因為PB⊥DM,?
∴PB⊥平面ADMN.
∵〈![]() ,
,![]() 〉的余角即是CD與平面ADMN所成的角.?
〉的余角即是CD與平面ADMN所成的角.?
∵cos〈![]() ,
,![]() 〉=
〉=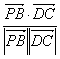 =
=![]() .?
.?
∴CD與平面ADMN所成的角為arcsin![]() .?
.?
點評:本題主要考查空間線線、線面關系、空間向量的概念與運算等基礎知識,同時考查空間想象能力.


科目:高中數學 來源: 題型:
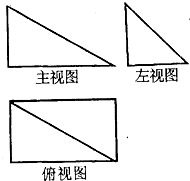 已知四棱錐P-ABCD的三視圖如右圖.該棱錐中,PA=AB=1,PD與平面ABCD所成角是30°,點F是PB的中點,點E在棱BC上移動.
已知四棱錐P-ABCD的三視圖如右圖.該棱錐中,PA=AB=1,PD與平面ABCD所成角是30°,點F是PB的中點,點E在棱BC上移動.查看答案和解析>>
科目:高中數學 來源:新課標高三數學空間圖形的基本關系與公理、空間圖形的平行關系專項訓練(河北) 題型:解答題
如右圖所示,在四棱錐P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,點F是PB的中點,點E在邊BC上移動.
 (1)求三棱錐E—PAD的體積;
(1)求三棱錐E—PAD的體積;
(2)當點E為BC的中點時,試判斷EF與平面PAC的位置關系,并說明理由;
(3)證明:無論點E在邊BC的何處,都有PE⊥AF.
查看答案和解析>>
科目:高中數學 來源:新課標高三數學空間圖形的平行關系、垂直關系專項訓練(河北) 題型:解答題
如右圖所示,在四棱錐P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,點F是PB的中點,點E在邊BC上移動.
(1)求三棱錐E—PAD的體積;
(2)當點E為BC的中點時,試判斷EF與平面PAC的位置關系,并說明理由;
(3)證明:無論點E在邊BC的何處,都有PE⊥AF.
查看答案和解析>>
科目:高中數學 來源: 題型:

(1)求證:BE⊥PD;
(2)求異面直線AE與CD所成角的大小.(用反三角函數表示)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com