
設![]() 是一常數,過點
是一常數,過點![]() 的直線與拋物線
的直線與拋物線![]() 交于相異兩點A、B,以線段AB為直經作圓H(H為圓心)。試證拋物線頂點在圓H的圓周上;并求圓H的面積最小時直線AB的方程.
交于相異兩點A、B,以線段AB為直經作圓H(H為圓心)。試證拋物線頂點在圓H的圓周上;并求圓H的面積最小時直線AB的方程.
Y

y2=2px
B
X
Q(2p,0) O
A
解法一:由題意,直線AB不能是水平線,
故可設直線方程為: 又設 消去x得
由此得 因此 故O必在圓H的圓周上. 又由題意圓心H( 由前已證,OH應是圓H的半徑,且 從而當k=0時,圓H的半徑最小,亦使圓H的面積最小. 此時,直線AB的方程為:x=2p. 解法二:由題意,直線AB不能是水平線,故可設直線方程為:ky=x-2p 又設 分別消去x,y得 故得A、B所在圓的方程 明顯地,O(0,0)滿足上面方程所表示的圓上, 又知A、B中點H的坐標為 故
而前面圓的方程可表示為 故|OH|為上面圓的半徑R,從而以AB為直徑的圓必過點O(0,0). 又 故當k=0時,R2最小,從而圓的面積最小,此時直線AB的方程為:x=2p. 解法三:同解法一得O必在圓H的圓周上 又直徑|AB|=
上式當 此時直線AB的方程為x=2p.
|


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
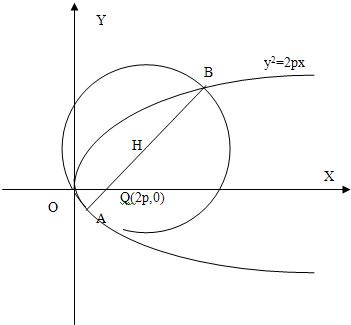 設p>0是一常數,過點Q(2p,0)的直線與拋物線y2=2px交于相異兩點A、B,以線段AB為直經作圓H(H為圓心).試證拋物線頂點在圓H的圓周上;并求圓H的面積最小時直線AB的方程.
設p>0是一常數,過點Q(2p,0)的直線與拋物線y2=2px交于相異兩點A、B,以線段AB為直經作圓H(H為圓心).試證拋物線頂點在圓H的圓周上;并求圓H的面積最小時直線AB的方程.查看答案和解析>>
科目:高中數學 來源:數學教研室 題型:044
Y
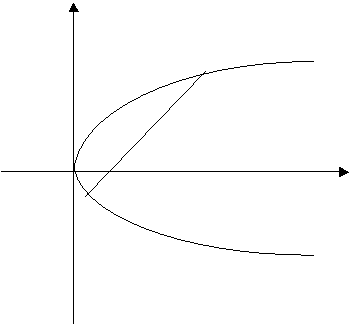
y2=2px
B
X
Q(2p,0) O
A
查看答案和解析>>
科目:高中數學 來源: 題型:
(04年重慶卷)(12分)
設![]() 是一常數,過點
是一常數,過點![]() 的直線與拋物線
的直線與拋物線![]() 交于相異兩點A、B,以線段AB為直經作圓H(H為圓心)
交于相異兩點A、B,以線段AB為直經作圓H(H為圓心)![]() 試證拋物線頂點在圓H的圓周上;并求圓H的面積最小時直線AB的方程
試證拋物線頂點在圓H的圓周上;并求圓H的面積最小時直線AB的方程![]()

查看答案和解析>>
科目:高中數學 來源:2004年重慶市高考數學試卷(文科)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com