
【題目】如圖,正方形![]() 是某城市的一個區域的示意圖,陰影部分為街道,各相鄰的兩紅綠燈之間的距離相等,
是某城市的一個區域的示意圖,陰影部分為街道,各相鄰的兩紅綠燈之間的距離相等,![]() 處為紅綠燈路口,紅綠燈統一設置如下:先直行綠燈30秒,再左轉綠燈30秒,然后是紅燈1分鐘,右轉不受紅綠燈影響,這樣獨立的循環運行.小明上學需沿街道從
處為紅綠燈路口,紅綠燈統一設置如下:先直行綠燈30秒,再左轉綠燈30秒,然后是紅燈1分鐘,右轉不受紅綠燈影響,這樣獨立的循環運行.小明上學需沿街道從![]() 處騎行到
處騎行到![]() 處(不考慮
處(不考慮![]() 處的紅綠燈),出發時的兩條路線(
處的紅綠燈),出發時的兩條路線(![]() )等可能選擇,且總是走最近路線.
)等可能選擇,且總是走最近路線.
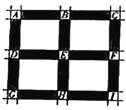
(1)請問小明上學的路線有多少種不同可能?
(2)在保證通過紅綠燈路口用時最短的前提下,小明優先直行,求小明騎行途中恰好經過![]() 處,且全程不等紅綠燈的概率;
處,且全程不等紅綠燈的概率;
(3)請你根據每條可能的路線中等紅綠燈的次數的均值,為小明設計一條最佳的上學路線,且應盡量避開哪條路線?
【答案】(1)6種;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)從4條街中選擇2條橫街即可;
(2)小明途中恰好經過![]() 處,共有4條路線,即
處,共有4條路線,即![]() ,
,![]() ,
,![]() ,
,![]() ,分別對4條路線進行分析計算概率;
,分別對4條路線進行分析計算概率;
(3)分別對小明上學的6條路線進行分析求均值,均值越大的應避免.
(1)路途中可以看成必須走過2條橫街和2條豎街,即從4條街中選擇2條橫街即可,所以路線總數為![]() 條.
條.
(2)小明途中恰好經過![]() 處,共有4條路線:
處,共有4條路線:
①當走![]() 時,全程不等紅綠燈的概率
時,全程不等紅綠燈的概率![]() ;
;
②當走![]() 時,全程不等紅綠燈的概率
時,全程不等紅綠燈的概率![]() ;
;
③當走![]() 時,全程不等紅綠燈的概率
時,全程不等紅綠燈的概率![]() ;
;
④當走![]() 時,全程不等紅綠燈的概率
時,全程不等紅綠燈的概率![]() .
.
所以途中恰好經過![]() 處,且全程不等信號燈的概率
處,且全程不等信號燈的概率
![]() .
.
(3)設以下第![]() 條的路線等信號燈的次數為變量
條的路線等信號燈的次數為變量![]() ,則
,則
①第一條:![]() ,則
,則![]() ;
;
②第二條:![]() ,則
,則![]() ;
;
③另外四條路線:![]() ;
;![]() ;
;
![]() ,則
,則![]()
綜上,小明上學的最佳路線為![]() ;應盡量避開
;應盡量避開![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上,
上,![]() ,試確定
,試確定![]() 的值,使
的值,使![]() 平面
平面![]() ;
;
(3)若![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() ,
,![]() ,直線
,直線![]() 、
、![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動點
,記動點![]() 的軌跡為曲線
的軌跡為曲線![]() 。
。
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,是否存在定點
兩點,是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 斜率之積為定值,若存在,求出
斜率之積為定值,若存在,求出![]() 坐標;若不存在,請說明理由。
坐標;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,AC⊥BC,且,AC=BC=2,D,E分別為AB,PB中點,PD⊥平面ABC,PD=3.
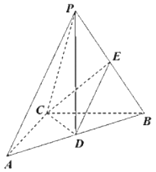
(1)求直線CE與直線PA夾角的余弦值;
(2)求直線PC與平面DEC夾角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 是自然對數的底數,
是自然對數的底數,![]() ).
).
(1)求函數![]() 的圖象在
的圖象在![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在區間
在區間![]() 上單調遞增,求實數
上單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 在區間
在區間![]() 上有兩個極值點
上有兩個極值點![]() ,且
,且![]() 恒成立,求滿足條件的
恒成立,求滿足條件的![]() 的最小值(極值點是指函數取極值時對應的自變量的值).
的最小值(極值點是指函數取極值時對應的自變量的值).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市一所醫院在某時間段為發燒超過38![]() 的病人特設發熱門診,該門診記錄了連續5天晝夜溫差
的病人特設發熱門診,該門診記錄了連續5天晝夜溫差![]() (
(![]() )與就診人數
)與就診人數![]() 的資料:
的資料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
晝夜溫差 | 8 | 10 | 13 | 12 | 7 |
就診人數 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相關系數
的相關系數![]() ,并說明晝夜溫差(
,并說明晝夜溫差(![]() )與就診人數
)與就診人數![]() 具有很強的線性相關關系.
具有很強的線性相關關系.
(2)求就診人數![]() (人)關于出晝夜溫差
(人)關于出晝夜溫差![]() (
(![]() )的線性回歸方程,預測晝夜溫差為9
)的線性回歸方程,預測晝夜溫差為9![]() 時的就診人數.
時的就診人數.
附:樣本![]()
![]() 的相關系數為
的相關系數為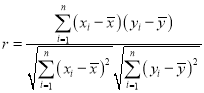 ,當
,當![]() 時認為兩個變量有很強的線性相關關系.
時認為兩個變量有很強的線性相關關系.
回歸直線方程為![]() ,其中
,其中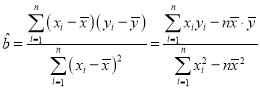 ,
,![]() .
.
參考數據:![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() .
.
(1)當![]() 時,直線
時,直線![]() 被圓
被圓![]() 截得的弦長為__________;
截得的弦長為__________;
(2)若在圓![]() 上存在一點
上存在一點![]() ,在直線
,在直線![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 的中點恰為坐標原點
的中點恰為坐標原點![]() ,則實數
,則實數![]() 的取值范圍是__________.
的取值范圍是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題:其中正確命題數是( )
A.在線性回歸模型中,相關系數![]() 表示解釋變量
表示解釋變量![]() 對于預報變量
對于預報變量![]() 變化的貢獻率,
變化的貢獻率,![]() 越接近于1,表示回歸效果越好
越接近于1,表示回歸效果越好
B.兩個變量相關性越強,則相關系數的絕對值就越接近于1
C.在回歸直線方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加一個單位時,預報變量
每增加一個單位時,預報變量![]() 平均減少0.5個單位
平均減少0.5個單位
D.對分類變量![]() 與
與![]() ,它們的隨機變量
,它們的隨機變量![]() 的觀測值來說,觀測值越小,“
的觀測值來說,觀測值越小,“![]() 與
與![]() 有關系”的把握程度越大
有關系”的把握程度越大
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據以往統計資料,某地車主購買甲種保險的概率為0.5,購買乙種保險但不購買甲種保險的概率為0.3.設各車主購買保險相互獨立.
(1)求該地1位車主至少購買甲、乙兩種保險中的1種的概率;
(2)X表示該地的100位車主中,甲、乙兩種保險都不購買的車主數,求X的均值和方差.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com