
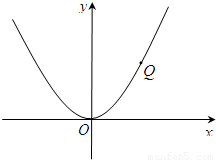
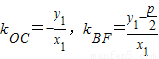 又OC⊥BF,∴
又OC⊥BF,∴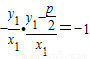 化簡得
化簡得 ,
,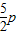 .
.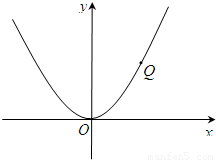
 ,設Q(x,y),假設存在直線y=b和圓Q截得弦長為定值,設兩交點為M、N,
,設Q(x,y),假設存在直線y=b和圓Q截得弦長為定值,設兩交點為M、N,
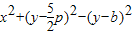
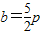 ,x2=2py∴MN=4P,即直線y=
,x2=2py∴MN=4P,即直線y=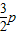 .
.

 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2013-2014學年人教版高考數學文科二輪專題復習提分訓練16練習卷(解析版) 題型:解答題
已知E(2,2)是拋物線C:y2=2px上一點,經過點(2,0)的直線l與拋物線C交于A,B兩點(不同于點E),直線EA,EB分別交直線x=-2于點M,N.
(1)求拋物線方程及其焦點坐標;
(2)已知O為原點,求證:∠MON為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com