
 )x+1,
)x+1, )+
)+ sin(2x+
sin(2x+ )時,g(x)在A上是單調遞增函數,求θ的取值范圍.
)時,g(x)在A上是單調遞增函數,求θ的取值范圍. )≠0,且函數f(x)的圖象關于點(
)≠0,且函數f(x)的圖象關于點( ,0)對稱,在x=π處取得最小值,試探討ω應該滿足的條件.
,0)對稱,在x=π處取得最小值,試探討ω應該滿足的條件.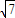 sin(2x+α)∈[-
sin(2x+α)∈[-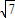 ,
,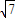 ],可得A,再根據g(x)的解析式結合題意可得tanθ≤-
],可得A,再根據g(x)的解析式結合題意可得tanθ≤- ,由此可得θ的取值范圍.
,由此可得θ的取值范圍. )≠0,可得f(x)=msinωx+ncosωx=
)≠0,可得f(x)=msinωx+ncosωx=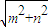 sin(ωx+φ),且 m2+n2≠0.由條件可得ω=4n-3,n∈N* ①,而且
sin(ωx+φ),且 m2+n2≠0.由條件可得ω=4n-3,n∈N* ①,而且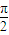 ,k∈z.
,k∈z.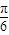 )+
)+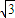 sin(2x+
sin(2x+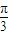 )=
)=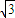 sin2x+2cos2x=
sin2x+2cos2x=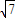 sin(2x+α)∈[-
sin(2x+α)∈[-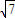 ,
,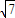 ],
],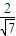 ,cosα=
,cosα=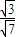 ,所以 A=[-
,所以 A=[-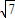 ,
,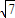 ]…(8分)
]…(8分)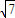 tanθ)x+1=
tanθ)x+1=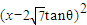 +1-28tan2θ,
+1-28tan2θ,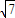 tanθ≤-
tanθ≤-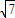 ,tanθ≤-
,tanθ≤- ,∴kπ-
,∴kπ- ≤θ≤kπ-arctan
≤θ≤kπ-arctan ,k∈z,
,k∈z,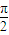 ,kπ-arctan
,kπ-arctan ],k∈z.(10)
],k∈z.(10) )≠0,∴a1•cosφ1+a2•cosφ2+…+an•cosφn =0
)≠0,∴a1•cosφ1+a2•cosφ2+…+an•cosφn =0 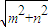 =sin(ωx+φ),且 m2+n2≠0.
=sin(ωx+φ),且 m2+n2≠0.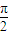 ,0)對稱,在x=π處取得最小值,∴(4n-3)
,0)對稱,在x=π處取得最小值,∴(4n-3)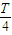 =π-
=π-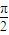 ,n∈N*.
,n∈N*.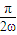 =
=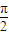 ,∴ω=4n-3,n∈N* ①.
,∴ω=4n-3,n∈N* ①.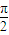 ,0)對稱可得 sin(
,0)對稱可得 sin(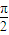 ω+φ)=0,故
ω+φ)=0,故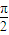 ω+φ=kπ,k∈z.
ω+φ=kπ,k∈z.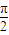 (4m-3)+φ=kπ,φ=kπ+
(4m-3)+φ=kπ,φ=kπ+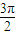 ,k∈z.
,k∈z.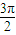 =2k′π+
=2k′π+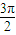 ,k′∈z.
,k′∈z.

 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:高中數學 來源: 題型:
 已知函數y=f(x)是定義在R上的奇函數,當x>0 時,f(x)的圖象如圖所示,則不等式x[f(x)-f(-x)]≤0 的解集為
已知函數y=f(x)是定義在R上的奇函數,當x>0 時,f(x)的圖象如圖所示,則不等式x[f(x)-f(-x)]≤0 的解集為查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com