
【題目】從一批草莓中,隨機抽取50個,其重量(單位:克)的頻數分布表如下:
分組(重量) |
|
|
|
|
須數(個) | 10 | 5 | 20 | 15 |
(1)根據頻數分布表計算草莓的重量在![]() 的頻率;
的頻率;
(2)用分層抽樣的方法從重量在![]() 和
和![]() 的草莓中共抽取5個,其中重量在
的草莓中共抽取5個,其中重量在![]() 的有幾個?
的有幾個?
(3)從(2)中抽出的5個草莓中任取2個,求重量在![]() 和
和![]() 中各有1個的概率.
中各有1個的概率.
【答案】(1)0.4;(2)2;(3)![]() .
.
【解析】
(1)用草莓的重量在![]() 的頻率除以樣本容量,即為所求;
的頻率除以樣本容量,即為所求;
(2)根據重量在![]() 的頻數所占的比例,求得重量在
的頻數所占的比例,求得重量在![]() 的草莓的個數;
的草莓的個數;
(3)用列舉法求出所有的基本事件的個數,再求出滿足條件的個數,即可得到所求事件的概率.
(1)重量在![]() 的頻率
的頻率![]() ;
;
(2)若采用分層抽樣的方法從重量在![]() 和
和![]() 的草莓中共抽取5個,則重量在
的草莓中共抽取5個,則重量在![]() 的個數為:
的個數為:![]() ;
;
(3)設在![]() 中抽取的2個草莓為
中抽取的2個草莓為![]() ,
,![]() ,在
,在![]() 中抽取的三個草莓分別為
中抽取的三個草莓分別為![]() ,
,![]() ,
,![]() ,從抽出的5個草莓中,任取2個共有
,從抽出的5個草莓中,任取2個共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 10種情況,
10種情況,
其中符合“重量在[80,85)和[95,100)中各有一個”的情況共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 6種;
6種;
設“抽出的5個草莓中,任取2個,求重量在![]() 和
和![]() 中各有一個”為事件
中各有一個”為事件![]() ,則事件
,則事件![]() 的概率.
的概率.![]() .
.


科目:高中數學 來源: 題型:
【題目】下列關于隨機變量及分布的說法正確的是( )
A.拋擲均勻硬幣一次,出現正面的次數是隨機變量
B.某人射擊時命中的概率為0.5,此人射擊三次命中的次數![]() 服從兩點分布
服從兩點分布
C.離散型隨機變量的分布列中,隨機變量取各個值的概率之和可以小于1
D.離散型隨機變量的各個可能值表示的事件是彼此互斥的
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,拋物線
,拋物線![]() :
: ![]() 與拋物線
與拋物線![]() :
: ![]() 異于原點
異于原點![]() 的交點為
的交點為![]() ,且拋物線
,且拋物線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(1)若直線![]() 與拋物線
與拋物線![]() 交于點
交于點![]() ,
, ![]() ,且
,且![]() ,求
,求![]() ;
;
(2)證明: ![]() 的面積與四邊形
的面積與四邊形![]() 的面積之比為定值.
的面積之比為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】1642年,帕斯卡發明了一種可以進行十進制加減法的機械計算機![]() 年,萊布尼茨改進了帕斯卡的計算機,但萊布尼茲認為十進制的運算在計算機上實現起來過于復雜,隨即提出了“二進制”數的概念
年,萊布尼茨改進了帕斯卡的計算機,但萊布尼茲認為十進制的運算在計算機上實現起來過于復雜,隨即提出了“二進制”數的概念![]() 之后,人們對進位制的效率問題進行了深入的研究
之后,人們對進位制的效率問題進行了深入的研究![]() 研究方法如下:對于正整數
研究方法如下:對于正整數![]() ,
,![]() ,我們準備
,我們準備![]() 張不同的卡片,其中寫有數字0,1,…,
張不同的卡片,其中寫有數字0,1,…,![]() 的卡片各有
的卡片各有![]() 張
張![]() 如果用這些卡片表示
如果用這些卡片表示![]() 位
位![]() 進制數,通過不同的卡片組合,這些卡片可以表示
進制數,通過不同的卡片組合,這些卡片可以表示![]() 個不同的整數
個不同的整數![]() 例如
例如![]() ,
,![]() 時,我們可以表示出
時,我們可以表示出![]() 共
共![]() 個不同的整數
個不同的整數![]() 假設卡片的總數
假設卡片的總數![]() 為一個定值,那么
為一個定值,那么![]() 進制的效率最高則意味著
進制的效率最高則意味著![]() 張卡片所表示的不同整數的個數
張卡片所表示的不同整數的個數![]() 最大
最大![]() 根據上述研究方法,幾進制的效率最高?
根據上述研究方法,幾進制的效率最高?![]()
![]()
A. 二進制 B. 三進制 C. 十進制 D. 十六進制
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,正確的個數是__________.(1)已知![]() ,則“
,則“![]() ”是“
”是“![]() ”的充分不必要條件;(2)已知
”的充分不必要條件;(2)已知![]() ,則“
,則“![]() ”是“
”是“![]() ”的必要不充分條件;(3)命題“p或q”為真命題,則“命題p”和“命題q”均為真命題;(4)命題“若
”的必要不充分條件;(3)命題“p或q”為真命題,則“命題p”和“命題q”均為真命題;(4)命題“若![]() ,則
,則![]() ”的逆否命題是真命題.
”的逆否命題是真命題.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 軸,直線
軸,直線![]() 交
交![]() 軸于
軸于![]() 點,
點,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 的面積的最大值為1.
的面積的最大值為1.
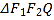
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條直線與橢圓
作兩條直線與橢圓![]() 分別交于
分別交于![]() 且使
且使![]() 軸,如圖,問四邊形
軸,如圖,問四邊形![]() 的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】柴靜《穹頂之下》的播出,讓大家對霧霾天氣的危害有了更進一步的認識,對于霧霾天氣的研究也漸漸活躍起來,某研究機構對春節燃放煙花爆竹的天數x與霧霾天數y進行統計分析,得出下表數據:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)試根據(2)求出的線性回歸方程,預測燃放煙花爆竹的天數為![]() 的霧霾天數.
的霧霾天數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com