
【題目】如圖,四邊形ABCD是平行四邊形,平面AED⊥平面ABCD,EF||AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G為BC的中點.
,DE=3,∠BAD=60,G為BC的中點.
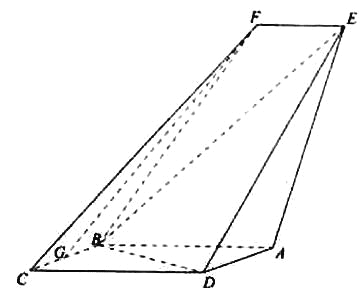
(Ⅰ)求證:FG||平面BED;
(Ⅱ)求證:平面BED⊥平面AED;
(Ⅲ)求直線EF與平面BED所成角的正弦值.
【答案】(Ⅰ)詳見解析(Ⅱ)詳見解析(Ⅲ)![]()
【解析】
試題(Ⅰ)證明線面平行,一般利用線面平行判定定理,即從線線平行出發給予證明,而線線平行尋找與論證,往往結合平幾知識,如本題構造一個平行四邊形:取![]() 的中點為
的中點為![]() ,可證四邊形
,可證四邊形![]() 是平行四邊形,從而得出
是平行四邊形,從而得出![]() (Ⅱ)面面垂直的證明,一般轉化為證線面垂直,而線面垂直的證明,往往需多次利用線面垂直判定與性質定理,而線線垂直的證明有時需要利用平幾條件,如本題可由余弦定理解出
(Ⅱ)面面垂直的證明,一般轉化為證線面垂直,而線面垂直的證明,往往需多次利用線面垂直判定與性質定理,而線線垂直的證明有時需要利用平幾條件,如本題可由余弦定理解出![]() ,即
,即![]() (Ⅲ)求線面角,關鍵作出射影,即面的垂線,可利用面面垂直的性質定理得到線面垂直,即面的垂線:過點
(Ⅲ)求線面角,關鍵作出射影,即面的垂線,可利用面面垂直的性質定理得到線面垂直,即面的垂線:過點![]() 作
作![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() ,從而直線
,從而直線![]() 與平面
與平面![]() 所成角即為
所成角即為![]() .再結合三角形可求得正弦值
.再結合三角形可求得正弦值
試題解析:(Ⅰ)證明:取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,在
,在![]() 中,因為
中,因為![]() 是
是![]() 的中點,所以
的中點,所以![]() 且
且![]() ,又因為
,又因為![]() ,所以
,所以![]() 且
且![]()
,即四邊形![]() 是平行四邊形,所以
是平行四邊形,所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)證明:在![]() 中,
中,![]() ,由余弦定理可
,由余弦定理可![]() ,進而可得
,進而可得![]() ,即
,即![]() ,又因為平面
,又因為平面![]() 平面
平面![]() 平面
平面![]() ;平面
;平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .又因為
.又因為![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅲ)解:因為![]() ,所以直線
,所以直線![]() 與平面
與平面![]() 所成角即為直線
所成角即為直線![]() 與平面
與平面![]() 所成角.過點
所成角.過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() ,又因為平面
,又因為平面![]() 平面
平面![]() ,由(Ⅱ)知
,由(Ⅱ)知![]() 平面
平面![]() ,所以直線
,所以直線![]() 與平面
與平面![]() 所成角即為
所成角即為![]() .在
.在![]() 中,
中,![]() ,由余弦定理可得
,由余弦定理可得![]() ,所以
,所以![]() ,因此
,因此![]() ,在
,在![]() 中,
中,![]() ,所以直線
,所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]()


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:高中數學 來源: 題型:
【題目】土筍凍是閩南種廣受歡迎的特色傳統風味小吃某小區超市銷售一款土筍凍,進價為每個15元,售價為每個20元.銷售的方案是當天進貨,當天銷售,未售出的全部由廠家以每個10元的價格回購處理.根據該小區以往的銷售情況,得到如圖所示的頻率分布直方圖:

(1)估算該小區土筍凍日需求量的平均數![]() (同一組中的數據用該組區間的中點值代表);
(同一組中的數據用該組區間的中點值代表);
(2)已知該超市某天購進了150個土筍凍,假設當天的需求量為![]() 個
個![]() 銷售利潤為
銷售利潤為![]() 元.
元.
(i)求關于![]() 的函數關系式;
的函數關系式;
(ii)結合上述頻率分布直方圖,以額率估計概率的思想,估計當天利潤![]() 不小于650元的概率.
不小于650元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,點
是菱形,點![]() 在線段PC上,且三棱錐
在線段PC上,且三棱錐![]() 的體積是四棱錐
的體積是四棱錐![]() 的體積的
的體積的![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
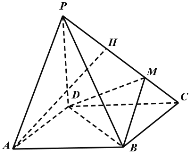
(1)若![]() 是
是![]() 的中點,證明:直線
的中點,證明:直線![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸,建立極坐標系,曲線
軸的非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為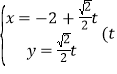 為參數
為參數![]() ,直線
,直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 兩點.
兩點.
(1)若點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值;
的值;
(2)求曲線![]() 的內接矩形周長的最大值.
的內接矩形周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC-A1B1C1中,點M,N分別為線段A1B,B1C的中點.

(1)求證:MN∥平面AA1C1C;
(2)若∠ABC=90°,AB=BC=2,AA1=3,求點B1到面A1BC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地隨著經濟的發展,居民收入逐年增長該地一建設銀行統計連續五年的儲蓄存款(年底余額)得到下表:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
儲蓄存款y(千億元) | 5 | 6 | 7 | 8 | 10 |
為便于計算,工作人員將上表的數據進行了處理(令![]()
![]() ),得到下表:
),得到下表:
時間t | 1 | 2 | 3 | 4 | 5 |
儲蓄存款z | 0 | 1 | 2 | 3 | 5 |
(1)求z關于t的線性回歸方程;
(2)通過(1)中的方程,求出y關于x的回歸方程;
(3)用所求回歸方程預測到2020年年底,該地儲蓄存款額可達多少?
附:線性回歸方程![]() ,其中
,其中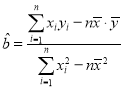 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 及圓
及圓![]() .
.
(1)若直線![]() 過點
過點![]() 且與圓心
且與圓心![]() 的距離為1,求直線
的距離為1,求直線![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,當
兩點,當![]() 時,求以線段
時,求以線段![]() 為直徑的圓
為直徑的圓![]() 的方程;
的方程;
(3)設直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,是否存在實數
兩點,是否存在實數![]() ,使得過點
,使得過點![]() 的直線
的直線![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出實數
?若存在,求出實數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com