解:(1)由f'(t)=0,
得(a
n-a
n-1)t=a
n+1-a
n(n≥2)
又a
2-a
1=t(t-1),t≠0且t≠1,
∴a
2-a
1≠0,
∴
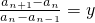
∴數列{a
n+1-a
n}是首項為t
2-t,公比為t的等比數列
(2)由(1)知a
n+1-a
n=t
n+1-t
n,
∴a
n-a
n-1=t
n-t
n-1,
∴a
n-1-a
n-2=t
n-1-t
n-2,
…
a
2-a
1=t
2-t,
上面n-1個等式相等并整理得a
n=t
n.(t≠0且t≠1)
b
n=a
nln|a
n|=t
n•ln|t
n|=nt
n•ln|t|.
∴S
n=(t+2•t
2+3•t
3++n•t
n)ln|t|,
tS
n=[t
2+2•t
3++(n-1)t
n+n•t
n+1]ln|t|,
兩式相減,并整理得
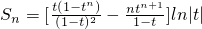
(3)∵
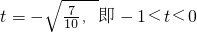
∴當n為偶數時,b
n=nt
nln|t|<0;
當n為奇數時,b
n=nt
nln|t|>0,∴最大項必須為奇數項
設最大項為:b
2k+1,則有
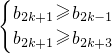
即:
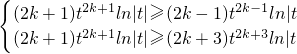
整理得
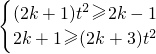
將
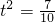
代入上式,解得
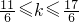
∵k∈N
+∴k=2,即數列{b
n}中的最大項是第5項
分析:(1)根據當x=t時,f(x)=

(a
n-a
n-1)x
2-(a
n+1-a
n)x(n≥2)取得極值,求導,得到f'(t)=0,即a
n-a
n-1)t=a
n+1-a
n(n≥2)整理可證;
(2)由(1),利用累加法即可求得數列{a
n}的通項公式,可求數列{b
n}的通項公式,再利用錯位相減法求和;
(3)根據(2)去絕對值符號,對n分奇偶討論,解不等式組即可證明結果.
點評:此題是個難題.考查等比數列的定義和通項公式,累加法求數列通項公式以及錯位相減法求數列的前n項和,體現了分類討論的思想.其中問題(3)是一個開放性問題,考查了同學們觀察、推理以及創造性地分析問題、解決問題的能力.

 (an-an-1)x2-(an+1-an)x(n≥2)取得極值?
(an-an-1)x2-(an+1-an)x(n≥2)取得極值?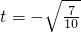 時,數列{bn}中是否存在最大項?如果存在,說明是第幾項;如果不存在,請說明理由?
時,數列{bn}中是否存在最大項?如果存在,說明是第幾項;如果不存在,請說明理由?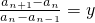
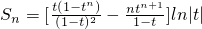
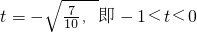
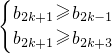
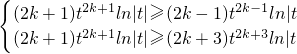
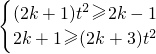
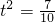 代入上式,解得
代入上式,解得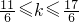
 (an-an-1)x2-(an+1-an)x(n≥2)取得極值,求導,得到f'(t)=0,即an-an-1)t=an+1-an(n≥2)整理可證;
(an-an-1)x2-(an+1-an)x(n≥2)取得極值,求導,得到f'(t)=0,即an-an-1)t=an+1-an(n≥2)整理可證;
