
解析:為了制定出居民用水量的標準,需要了解廣大居民的實際月用水量大部分在什么數值范圍內.但由于居民戶較多,全部調查不易操作,故可采取抽樣調查的方式獲取一個有代表性的樣本,然后通過樣本的情況估計所有居民的月用水量,以便制定出這個標準.
很顯然,如果標準太高,會影響居民的日常生活;如果標準太低,則不利于節水.為了確定一個較合理的標準,必須先了解居民日常用水的分布情況,比如月平均用水量在哪個范圍內的居民最多,他們占全市居民的百分比情況等.
由于城市居戶較多,通常采用抽樣調查的方式,通過分析樣本數據來估計全市居民用水量的分布情況.假設通過抽樣我們獲得了100位居民今年的月均用水量(單位:t):
100位居民2006年的月均用水量(單位:t):
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
面對這些隨意記錄的數據,除了發現月用水量的最大值是4.3和最小值是0.2之外,很難再看出其他信息.為此我們需要對這些數據進行分析整理.分析數據的一種最基本的方法是用圖(即頻率分布直方圖)將它們畫出來,以便從數據中提取信息和傳遞信息,或者是用緊湊的表格(即頻率分布表)改變數據的排列方式.下圖是100位居民2006年的月均用水量的頻率分布表:
分組 | 頻數 | 頻率 |
[0,0.5) | 4 | 0.04 |
[0.5,1) | 8 | 0.08 |
[1,1.5) | 15 | 0.15 |
[1.5,2) | 22 | 0.22 |
[2,2.5) | 25 | 0.25 |
[2.5,3) | 14 | 0.14 |
[3,3.5) | 6 | 0.06 |
[3.5,4) | 4 | 0.04 |
[4,4.5) | 2 | 0.02 |
合計 | 100 | 1.00 |
頻率分布直方圖如下:
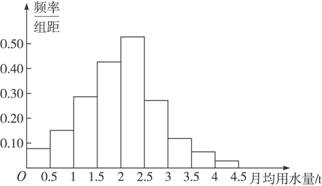
上面的圖和表顯示了樣本數據落在各個小組的比例大小.從中我們可以看到,月用水量在區間[2, 2.5]內的居民最多,在[1.5, 2]的次之,大部分居民的月用水量都在[1, 3]之間,其中月用水量在3 t以上的居民所占的比例為6%+4%+2%=12%,即大約占12%的居民月用水量在3 t以上,88%的居民月用水量在3 t以下.因此居民月用水量標準定為3 t是一個可以考慮的標準.


科目:高中數學 來源: 題型:
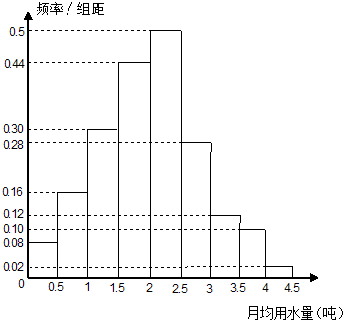 我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出.某市政府為了節約生活用水,計劃在本市試行居民生活用水定額管理,為此市政府首先采用抽樣調查的方法獲得了n位居民某年的月均用水量(單位:噸).根據所得的n個數據按照區間[0,0.5),[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5]進行分組,得到頻率分布直方圖如圖
我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出.某市政府為了節約生活用水,計劃在本市試行居民生活用水定額管理,為此市政府首先采用抽樣調查的方法獲得了n位居民某年的月均用水量(單位:噸).根據所得的n個數據按照區間[0,0.5),[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5]進行分組,得到頻率分布直方圖如圖查看答案和解析>>
科目:高中數學 來源: 題型:
 我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出.某市政府為了節約生活用水,計劃在本市試行居民生活用水定額管理,即確定一個居民月用水量的標準.為了確定一個較為合理的標準,必須先了解全市居民日常用水量的分布情況.現采用抽樣調查的方式,獲得了n位居民某年的月均用水量(單位:t),樣本統計結果如圖表:
我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出.某市政府為了節約生活用水,計劃在本市試行居民生活用水定額管理,即確定一個居民月用水量的標準.為了確定一個較為合理的標準,必須先了解全市居民日常用水量的分布情況.現采用抽樣調查的方式,獲得了n位居民某年的月均用水量(單位:t),樣本統計結果如圖表:| 分組 | 頻數 | 頻率 |
| [0,1) | 25 | a |
| [1,2) | 38 38 |
0.19 |
| [2,3) | 50 | b |
| [3,4) | 46 46 |
0.23 |
| [4,5) | 36 36 |
0.18 |
| [5,6] | 5 | 0.025 0.025 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河北省石家莊市高三第二次模擬理科數學試卷(解析版) 題型:解答題
我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出.某市為了節約生活用水,計劃在本市試行居民生活用水定額管理(即確定一個居民月均用水量標準〜用水量不超過a的部分按照平價收費,超過a的部分按照議價收費).為了較為合理地確定出這個標準,通過抽樣獲得了 100位居民某年的月均用水量(單位:t),制作了頻率分布直方圖,
(I)由于某種原因頻率分布直方圖部分數據丟失,請在圖中將其補充完整;
(II)用樣本估計總體,如果希望80%的居民每月的用水量不超出標準&則月均用水量的最低標準定為多少噸,并說明理由;
(III)若將頻率視為概率,現從該市某大型生活社區隨機調查3位居民的月均用水量(看作有放回的抽樣),其中月均用水量不超過(II)中最低標準的人數為x,求x的分布列和均值.

查看答案和解析>>
科目:高中數學 來源:2013屆四川省高二下學期期中(文理)數學試卷(解析版) 題型:解答題
(文)我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出。某市政府為了節約生活用水,計劃在本市試行居民生活用水定額管理,即確定一個居民月用水量的標準。為了確定一個較為合理的標準,必須先了解全市居民日常用水量的分布情況。現采用抽樣調查的方式,獲得了n位居民某年的月均用水量(單位:t),樣本統計結果如下圖表:

(1)分別求出n,a,b的值;
(2)若從樣本中月均用水量在[5,6](單位:t)的5位居民中任選2人作進一步的調查研究,求月均用水量最多的居民被選中的頻率(5位居民的月均用水量均不相等。)
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省海珠區高三第一次綜合測試數學理卷 題型:解答題
(本小題滿分12分)
我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出.某市政府為了節約生活用水,計劃在本市試行居民生活用水定額管理,為此市政府首先采用抽樣調查的方法獲得了 位居民某年的月均用水量(單位:噸).根據所得的
位居民某年的月均用水量(單位:噸).根據所得的 個數據按照區間
個數據按照區間 進行分組,得到頻率分布直方圖如圖
進行分組,得到頻率分布直方圖如圖
(1)若已知 位居民中月均用水量小于1噸的人數是12,求
位居民中月均用水量小于1噸的人數是12,求 位居民中月均用水量分別在區間
位居民中月均用水量分別在區間 和
和 內的人數;
內的人數;
(2)在該市居民中隨意抽取10位,求至少有2位居民月均用水量在區間 或
或 內的概率.(精確到0.01.參考數據:
內的概率.(精確到0.01.參考數據: )
)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com