
【題目】心理學家發現,學生的接受能力依賴于老師引入概念和描述問題所用的時間,上課開始時,學生的興趣激增,中間有一段不太長的時間,學生的興趣保持較理想的狀態,隨后學生的注意力開始分散,并趨于穩定.分析結果和實驗表明,設提出和講述概念的時間為![]() (單位:分),學生的接受能力為
(單位:分),學生的接受能力為![]() (
(![]() 值越大,表示接受能力越強),
值越大,表示接受能力越強),
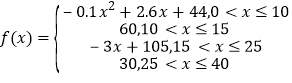
(1)開講后多少分鐘,學生的接受能力最強?能維持多少時間?
(2)試比較開講后5分鐘、20分鐘、35分鐘,學生的接受能力的大小;(3)若一個數學難題,需要56的接受能力以及12分鐘時間,老師能否及時在學生一直達到所需接受能力的狀態下講述完這個難題?
【答案】(1)開講后10分鐘,學生的接受能力最強,并能維持5分鐘.(2)從大小依次是開講后5分鐘、20分鐘、35分鐘的接受能力(3)不能
【解析】試題分析:(1)求學生的接受能力最強其實就是要求分段函數的最大值,方法是分別求出各段的最大值取其最大即可;(2)比較![]() 分鐘、
分鐘、![]() 分鐘、
分鐘、![]() 分鐘學生的接受能力大小,方法是把
分鐘學生的接受能力大小,方法是把![]() 代入第一段函數中,而
代入第一段函數中,而![]() 要代入到第三段函數中,
要代入到第三段函數中,![]() 代入第四段函數,比較大小即可;(3)在每一段上解不等式
代入第四段函數,比較大小即可;(3)在每一段上解不等式![]() ,求出滿足條件的
,求出滿足條件的![]() ,從而得到接受能力
,從而得到接受能力![]() 及以上的時間,然后與
及以上的時間,然后與![]() 進行比較即可.
進行比較即可.
試題解析:(Ⅰ)由題意可知:
![]()
所以當X=10時, ![]() 的最大值是60,
的最大值是60,
又![]() ,
, ![]() =60
=60
所以開講后10分鐘,學生的接受能力最強,并能維持5分鐘.
(Ⅱ)由題意可知:![]()
所以開講后5分鐘、20分鐘、35分鐘的學生的接受能力從大小依次是
開講后5分鐘、20分鐘、35分鐘的接受能力;
(Ⅲ)由題意可知:
當 ![]()
解得:![]()
當![]()
![]() =60>56,滿足要求;
=60>56,滿足要求;
當![]() ,
,![]()
解得:![]()
因此接受能力56及以上的時間是![]() 分鐘小于12分鐘.
分鐘小于12分鐘.
所以老師不能在所需的接受能力和時間狀態下講述完這個難題 .


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若對![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)記![]() ,那么當
,那么當![]() 時,是否存在區間
時,是否存在區間![]() 使得函數在區間
使得函數在區間![]() 上的值域恰好為
上的值域恰好為![]() ?若存在,請求出區間
?若存在,請求出區間![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一座大橋既是交通擁擠地段,又是事故多發地段,為了保證安全,交通部門規定:大橋上的車距![]() 與車速
與車速![]() 和車長
和車長![]() 的關系滿足
的關系滿足![]() 為正的常數).假定車身長為
為正的常數).假定車身長為![]() ,當車速為
,當車速為![]() 時,車距為
時,車距為![]() 個車身長.
個車身長.
(1)寫出車距![]() 關于車速
關于車速![]() 的函數關系式;
的函數關系式;
(2)應規定怎樣的車速,才能使大橋上每小時通過的車輛最多?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐P-ABCD中,底面是邊長為a的正方形,側棱PD=a,PA=PC=![]() a,
a,
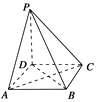
(1)求證:PD⊥平面ABCD;
(2)求證:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在12件同類型的零件中有2件次品,抽取3次進行檢驗,每次抽取1件,并且取出后不再放回,若以ξ和η分別表示取到的次品數和正品數.
(1)求ξ的分布列、均值和方差;
(2)求η的分布列、均值和方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點E為正方形ABCD邊CD上異于點C,D的動點,將△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,則下列三個說法中正確的個數是( )

①存在點E使得直線SA⊥平面SBC
②平面SBC內存在直線與SA平行
③平面ABCE內存在直線與平面SAE平行
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() (
(![]() ),焦點
),焦點![]() 到準線的距離為
到準線的距離為![]() ,過點
,過點![]()
![]() 作直線
作直線![]() 交拋物線
交拋物線![]() 于點
于點![]() (點
(點![]() 在第一象限).
在第一象限).
(Ⅰ)若點![]() 焦點
焦點![]() 重合,且弦長
重合,且弦長![]() ,求直線
,求直線![]() 的方程;
的方程;
(Ⅱ)若點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,直線
,直線![]() 交x軸于點
交x軸于點![]() ,且
,且![]() ,求證:點B的坐標是
,求證:點B的坐標是![]() ,并求點
,并求點![]() 到直線
到直線![]() 的距離
的距離![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,
,![]() 是橢圓的焦點,直線
是橢圓的焦點,直線![]() 的斜率為
的斜率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)設過點![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() 兩點,當
兩點,當![]() 的面積最大時,求
的面積最大時,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com