
【題目】如圖,在三棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,點
,點![]() 是棱
是棱![]() 的中點,
的中點,![]() ,點
,點![]() 是棱
是棱![]() 上一點,且
上一點,且![]() .
.
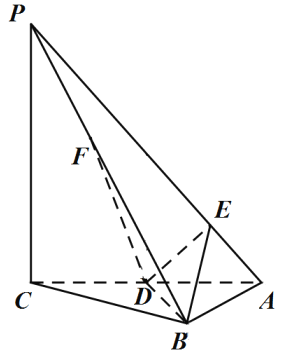
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)證明![]() 平面
平面![]() ,可得出
,可得出![]() ,再證明
,再證明![]() 可得出
可得出![]() ,利用線面垂直的判定定理可得出結論;
,利用線面垂直的判定定理可得出結論;
(2)過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() ,然后以點
,然后以點![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 、
、![]() 、
、![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,計算出
,計算出![]() 的坐標,并計算出平面
的坐標,并計算出平面![]() 的法向量,利用空間向量法能計算出直線
的法向量,利用空間向量法能計算出直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
(1)因為![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() ,
,
因為![]() ,
,![]() ,
,![]() ,
,
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,又
,又![]() ,
,![]() 平面
平面![]() ;
;
(2)因為![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() ,因為
,因為![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因為![]() ,故可以
,故可以![]() 、
、![]() 、
、![]() 分別作為
分別作為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
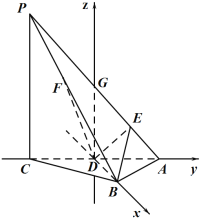
則部分點坐標為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,
因為點![]() 在棱
在棱![]() 上,且
上,且![]() ,則
,則![]() ,
,
則![]() ,即有
,即有![]() ,即
,即 ,
,
由(1)知![]() 平面
平面![]() ,則
,則![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,則
,則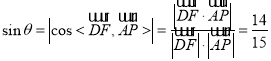 ,
,
即直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源: 題型:
【題目】某工廠生產的產品中分正品與次品,正品重![]() ,次品重
,次品重![]() ,現有5袋產品(每袋裝有10個產品),已知其中有且只有一袋次品(10個產品均為次品)如果將5袋產品以1~5編號,第
,現有5袋產品(每袋裝有10個產品),已知其中有且只有一袋次品(10個產品均為次品)如果將5袋產品以1~5編號,第![]() 袋取出
袋取出![]() 個產品(
個產品(![]() ),并將取出的產品一起用秤(可以稱出物體重量的工具)稱出其重量
),并將取出的產品一起用秤(可以稱出物體重量的工具)稱出其重量![]() ,若次品所在的袋子的編號是2,此時的重量
,若次品所在的袋子的編號是2,此時的重量![]() _________
_________![]() ;若次品所在的袋子的編號是
;若次品所在的袋子的編號是![]() ,此時的重量
,此時的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】質檢部門為了解某企業生產的一-種圓柱形零件的質量情況,隨機抽檢了100個零件,得到這些零件的橫截面直徑d(單位:![]() )的頻率分布表如下:
)的頻率分布表如下:
d的分組 |
|
|
|
|
|
零件數 | 12 | 38 | 38 | 10 | 2 |
(1)試估計這個企業生產的這類零件的橫截面直徑不低于![]() 的概率;
的概率;
(2)求這個企業生產的這類零件的橫截面直徑的平均數與標準差的估計值(同一組中的數據用該區間的中點值為代表).(精確到0.01)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某手機商城2018年華為、蘋果、三星三種品牌的手機各季度銷量的百分比堆積圖(如:第三季度華為銷量約占50%,蘋果銷量約占20%,三星銷量約占30%).根據該圖,以下結論中一定正確的是( )
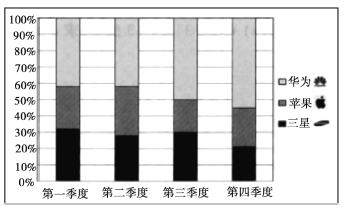
A.華為的全年銷量最大B.蘋果第二季度的銷量大于第三季度的銷量
C.華為銷量最大的是第四季度D.三星銷量最小的是第四季度
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自由購是一種通過自助結算購物的形式.某大型超市為調查顧客自由購的使用情況,隨機抽取了100人,調查結果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人數 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人數 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)現隨機抽取1名顧客,試估計該顧客年齡在[30,50)且未使用自由購的概率;
(2)從被抽取的年齡在[50,70]使用的自由購顧客中,隨機抽取2人進一步了解情況,求這2人年齡都在[50,60)的概率;
(3)為鼓勵顧客使用自由購,該超市擬對使用自由購顧客贈送1個環保購物袋.若某日該超市預計有5000人購物,試估計該超市當天至少應準備多少個環保購物袋?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2acoskπlnx(k∈N*,a∈R且a>0).
(1)討論函數f(x)的單調性;
(2)若k=2018,關于x的方程f(x)=2ax有唯一解,求a的值;
(3)當k=2019時,證明:對一切x∈(0,+∞),都有![]() 成立.
成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com