
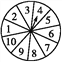
【題目】有一個轉盤游戲,轉盤被平均分成10等份(如圖所示),轉動轉盤,當轉盤停止后,指針指向的數字即為轉出的數字.游戲規則如下:兩個人參加,先確定猜數方案,甲轉動轉盤,乙猜,若猜出的結果與轉盤轉出的數字所表示的特征相符,則乙獲勝,否則甲獲勝.猜數方案從以下三種方案中選一種:
A.猜“是奇數”或“是偶數”
B.猜“是4的整數倍數”或“不是4的整數倍數”
C.猜“是大于4的數”或“不是大于4的數”
請回答下列問題:
(1)如果你是乙,為了盡可能獲勝,你將選擇哪種猜數方案,并且怎樣猜?為什么?
(2)為了保證游戲的公平性,你認為應制定哪種猜數方案?為什么?
(3)請你設計一種其他的猜數方案,并保證游戲的公平性.
【答案】(1) 應選方案B ,猜“不是4的整數倍數”;(2) 應當選擇方案A;
(3) 可以設計為:猜“是大于5的數”或“不是大于5的數”
【解析】試題分析:(1) 方案A中“是奇數”或“是偶數”的概率均為![]() ,案B中“不是4的整數倍數”的概率為
,案B中“不是4的整數倍數”的概率為![]() ,“是4的整數倍數”的概率為
,“是4的整數倍數”的概率為![]() ,方案C中“是大于4的數”的概率為
,方案C中“是大于4的數”的概率為![]() ,“不是大于4的數”的概率為
,“不是大于4的數”的概率為![]() ,乙為了盡可能獲勝,應選方案B,猜“不是4的整數倍數”. (2) 為了保證游戲的公平性,應當選擇方案A. “是奇數”或“是偶數”的概率均為
,乙為了盡可能獲勝,應選方案B,猜“不是4的整數倍數”. (2) 為了保證游戲的公平性,應當選擇方案A. “是奇數”或“是偶數”的概率均為![]() (3) “是大于5的數”或“不是大于5的數”發生的概率是一樣的,也可以保證游戲的公平性
(3) “是大于5的數”或“不是大于5的數”發生的概率是一樣的,也可以保證游戲的公平性
試題解析:
(1)如題圖,方案A中“是奇數”或“是偶數”的概率均為![]() =0.5;方案B中“不是4的整數倍數”的概率為
=0.5;方案B中“不是4的整數倍數”的概率為![]() =0.8,“是4的整數倍數”的概率為
=0.8,“是4的整數倍數”的概率為![]() =0.2;方案C中“是大于4的數”的概率為
=0.2;方案C中“是大于4的數”的概率為![]() =0.6,“不是大于4的數”的概率為
=0.6,“不是大于4的數”的概率為![]() =0.4.乙為了盡可能獲勝,應選方案B,猜“不是4的整數倍數”.
=0.4.乙為了盡可能獲勝,應選方案B,猜“不是4的整數倍數”.
(2)為了保證游戲的公平性,應當選擇方案A.因為方案A猜“是奇數”或“是偶數”的概率均為0.5,從而保證了該游戲是公平的.
(3)可以設計為:猜“是大于5的數”或“不是大于5的數”,此方案也可以保證游戲的公平性.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某市的3個區共有高中學生20 000人,且3個區的高中學生人數之比為2∶3∶5,現要從所有學生中抽取一個容量為200的樣本,調查該市高中學生的視力情況,試寫出抽樣過程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人做游戲,下列游戲不公平的是( )
A. 拋擲一枚骰子,向上的點數為奇數則甲獲勝,向上的點數為偶數則乙獲勝
B. 同時拋擲兩枚硬幣,恰有一枚正面向上則甲獲勝,兩枚都正面向上則乙獲勝
C. 從一副不含大小王的撲克牌中抽一張,撲克牌是紅色的則甲獲勝,撲克牌是黑色的則乙獲勝
D. 甲、乙兩人各寫一個數字1或2,如果兩人寫的數字相同甲獲勝,否則乙獲勝
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)在如圖所示的五面體中,面![]() 為直角梯形,
為直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是邊長為2的正三角形.
是邊長為2的正三角形.
(1)證明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如下五個命題:
①在線性回歸模型中, ![]() 表示解釋變量對于預報變量變化的貢獻率,在對女大學生的身高預報體重的回歸分析數據中,算得
表示解釋變量對于預報變量變化的貢獻率,在對女大學生的身高預報體重的回歸分析數據中,算得![]() ,表明“女大學生的體重差異有64%是由身高引起的”
,表明“女大學生的體重差異有64%是由身高引起的”
②隨機變量的方差和標準差都反映了隨機變量取值偏離于均值的平均程度,方差或標準差越小,則隨機變量偏離于均值的平均程度越大;
③正態曲線關于直線![]() 對稱,這個曲線只有當
對稱,這個曲線只有當![]() 時,才在
時,才在![]() 軸上方;
軸上方;
④正態曲線的對稱軸由![]() 確定,當
確定,當![]() 一定時,曲線的形狀由
一定時,曲線的形狀由![]() 決定,并且
決定,并且![]() 越大,曲線越“矮胖”;
越大,曲線越“矮胖”;
⑤若隨機變量![]() ,且
,且![]() 則
則![]() ;
;
其中正確命題的序號是
A. ②③ B. ①④⑤ C. ①④ D. ①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代名詞“芻童”原來是草堆的意思,古代用它作為長方體棱臺(上、下底面均為矩形額棱臺)的專用術語,關于“芻童”體積計算的描述,《九章算術》注曰:“倍上表,下表從之,亦倍小表,上表從之,各以其廣乘之,并,以高若深乘之,皆六面一.”其計算方法是:將上底面的長乘二,與下底面的長相加,再與上底面的寬相乘;將下底面的長乘二,與上底面的長相加,再與下底面的寬相乘;把這兩個數值相加,與高相乘,再取其六分之一,以此算法,現有上下底面為相似矩形的棱臺,相似比為![]() ,高為3,且上底面的周長為6,則該棱臺的體積的最大值是( )
,高為3,且上底面的周長為6,則該棱臺的體積的最大值是( )
A. 14 B. 56 C. ![]() D. 63
D. 63
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓O1和圓O2的極坐標方程分別為ρ=2,ρ2-2![]() ρcos(θ-
ρcos(θ-![]() )=2.
)=2.
(1)把圓O1和圓O2的極坐標方程化為直角坐標方程;
(2)設兩圓交點分別為A、B,求直線AB的參數方程,并利用直線AB的參數方程求兩圓的公共弦長|AB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() ),以橢圓內一點
),以橢圓內一點![]() 為中點作弦
為中點作弦![]() ,設線段
,設線段![]() 的中垂線與橢圓相交于
的中垂線與橢圓相交于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)求橢圓的離心率;
(Ⅱ)試判斷是否存在這樣的![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一個圓上,并說明理由.
在同一個圓上,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com