
已知二次函數f(x)=px2+qx(p≠0),其導函數為f'(x)=6x-2,數列{an}的前n項和為Sn,點(n,Sn)(n∈N*)均在函數y=f(x)的圖象上.
(1)求數列{an}的通項公式.
(2)若cn= (an+2),2b1+22b2+23b3+…+2nbn=cn,求數列{bn}的通項公式.
(an+2),2b1+22b2+23b3+…+2nbn=cn,求數列{bn}的通項公式.
(1) an=6n-5 (2) bn=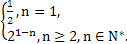
【解析】【思路點撥】(1)根據二次函數的導函數為f'(x)=6x-2,可求f(x)=3x2-2x,所以Sn=3n2-2n.由Sn可求an.
(2)根據an求cn,求出cn代入2b1+22b2+23b3+…+2nbn=cn中可求出bn,注意n=1與n≥2的討論.
【解析】
(1)已知二次函數f(x)=px2+qx(p≠0),
則f'(x)=2px+q=6x-2,故p=3,q=-2,
所以f(x)=3x2-2x.
點(n,Sn)(n∈N*)均在函數y=f(x)的圖象上,
則Sn=3n2-2n,當n=1時,a1=S1=1;
當n≥2時,an=Sn-Sn-1=6n-5,
故數列{an}的通項公式:an=6n-5.
(2)由(1)得,cn=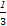 (an+2)=2n-1,
(an+2)=2n-1,
2b1+22b2+23b3+…+2nbn=2n-1,
當n=1時,b1=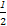 ,
,
當n≥2時,2b1+22b2+23b3+…+2n-1bn-1+2nbn
=2n-1,
2b1+22b2+23b3+…+2n-1bn-1=2(n-1)-1,
兩式相減得:bn=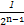 =21-n,
=21-n,
故數列{bn}的通項公式:bn=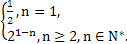


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2014年高考數學全程總復習課時提升作業二十二第三章第六節練習卷(解析版) 題型:選擇題
已知y=f(x)是奇函數,且圖象關于x=3對稱,f(1)=1,cosx-sinx=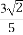 ,則f(
,則f(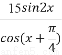 )=( )
)=( )
(A)-1 (B)0 (C)1 (D)2
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業二十七第四章第三節練習卷(解析版) 題型:填空題
已知平面向量a=(x1,y1),b=(x2,y2),若|a|=2,|b|=3,a·b=-6,則 = .
= .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十第五章第一節練習卷(解析版) 題型:解答題
數列{an}滿足:a1=1,an+1=3an+2n+1(n∈N*),求{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十第五章第一節練習卷(解析版) 題型:選擇題
已知數列{an}中,a1=1,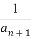 =
= +3(n∈N*),則a10=( )
+3(n∈N*),則a10=( )
(A)28(B)33(C)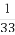 (D)
(D)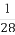
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十四第五章第五節練習卷(解析版) 題型:選擇題
等差數列{an}的公差為3,若a2, a4,a8成等比數列,則a4=( )
(A)8 (B)10 (C)12 (D)16
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十五第六章第一節練習卷(解析版) 題型:選擇題
若x>y>z>1,則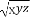 ,
,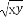 ,
,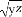 ,
,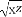 中最大的是( )
中最大的是( )
(A)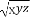 (B)
(B)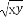
(C)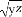 (D)
(D)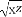
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com