
【題目】已知空間幾何體![]() 中,
中,![]() 與
與![]() 均為邊長為
均為邊長為![]() 的等邊三角形,
的等邊三角形,![]() 為腰長為
為腰長為![]() 的等腰三角形,平面
的等腰三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
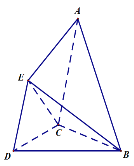
(1)試在平面![]() 內作一條直線,使直線上任意一點
內作一條直線,使直線上任意一點![]() 與
與![]() 的連線
的連線![]() 均與平面
均與平面![]() 平行,并給出詳細證明
平行,并給出詳細證明
(2)求點![]() 到平面
到平面![]() 的距離
的距離
【答案】(1)見解析;(2)![]()
【解析】
(1)取BC和BD的中點H、G,利用面面平行的判斷定理證得平面CDE平行平面AHG即可求得結果;
(2)分別求得三角形ABC和CDE的面積以及求得E到平面ABC的距離,再利用等體積法![]() 即可求得
即可求得![]() 到平面
到平面![]() 的距離.
的距離.
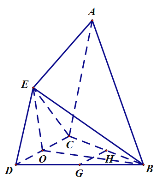
如圖所示:取BC和BD的中點H、G,連接HG,HG為所求直線,
證明如下:因為BC和BD的中點H、G,所以![]() ,
,
又平面![]() 平面
平面![]() ,且
,且![]() 平面BCD
平面BCD
又平面![]() 平面
平面![]() .
.![]() ,得
,得![]() ,
,
所以![]() ,即
,即![]()
所以![]() ,所以直線HG上任意一點
,所以直線HG上任意一點![]() 與
與![]() 的連線
的連線![]() 均與平面
均與平面![]() 平行.
平行.
由(1)可得![]() ,即
,即![]() 平面ABC
平面ABC
所以點E到平面ABC的距離和點O到平面ABC的距離相等,記為![]()
三角形ABC的面積![]()
而三角形ACE的面積![]()
用等體積法![]() 可得:
可得:
![]()


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 邊的中點,以
邊的中點,以![]() 為折痕把
為折痕把![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且
的位置,且![]() ..
..
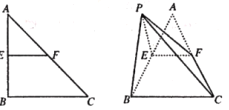
(Ⅰ)證明:![]() 平面
平面![]() ;
;
(Ⅱ)設![]() 為線段
為線段![]() 上動點,求直線
上動點,求直線![]() 與平面
與平面![]() 所成角的正弦值的最大值.
所成角的正弦值的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】獎飯店推出甲.乙兩種新菜品,為了了解兩種菜品的受歡迎程度,現統計一周內兩種菜品每天的銷售量,得到下面的莖葉圖.下列說法中,不正確的是( )
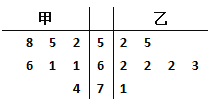
A.甲菜品銷售量的眾數比乙菜品銷售量的眾數小
B.甲菜品銷售量的中位數比乙菜品銷售量的中位數小
C.甲菜品銷售量的平均值比乙菜品銷售量的平均值大
D.甲菜品銷售量的方差比乙菜品銷售量的方差大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,點
,點![]() 在線段
在線段![]() 上.
上.
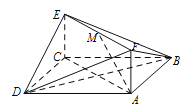
(Ⅰ)若![]() 為
為![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)證明:存在點![]() ,使得
,使得![]() 平面
平面![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店剛剛上市了《中國古代數學史》,銷售前該書店擬定了5種單價進行試銷,每種單價(![]() 元)試銷l天,得到如表單價
元)試銷l天,得到如表單價![]() (元)與銷量
(元)與銷量![]() (冊)數據:
(冊)數據:
單價 | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
(l)根據表中數據,請建立![]() 關于
關于![]() 的回歸直線方程:
的回歸直線方程:
(2)預計今后的銷售中,銷量![]() (冊)與單價
(冊)與單價![]() (元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
(元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
附: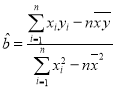 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,數列A:
,數列A:![]() ,
,![]() ,…
,…![]() 中的項均為不大于
中的項均為不大于![]() 的正整數.
的正整數.![]() 表示
表示![]() ,
,![]() ,…
,…![]() 中
中![]() 的個數(
的個數(![]() ).定義變換
).定義變換![]() ,
,![]() 將數列
將數列![]() 變成數列
變成數列![]() :
:![]() ,
,![]() ,…
,…![]() 其中
其中![]() .
.
(1)若![]() ,對數列
,對數列![]() :
:![]() ,寫出
,寫出![]() 的值;
的值;
(2)已知對任意的![]() (
(![]() ),存在
),存在![]() 中的項
中的項![]() ,使得
,使得![]() .求證:
.求證:![]() (
(![]() )的充分必要條件為
)的充分必要條件為![]() (
(![]() );
);
(3)若![]() ,對于數列
,對于數列![]() :
:![]() ,
,![]() ,…
,…![]() ,令
,令![]() :
:![]() ,求證:
,求證:![]() (
(![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知函數![]() 的零點構成一個公差為
的零點構成一個公差為![]() 的等差數列,把函數
的等差數列,把函數![]() 的圖像沿
的圖像沿![]() 軸向左平移
軸向左平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖像,關于函數
的圖像,關于函數![]() ,下列說法正確的是( )
,下列說法正確的是( )
A. 在![]() 上是增函數
上是增函數
B. 其圖像關于![]() 對稱
對稱
C. 函數![]() 是奇函數
是奇函數
D. 在區間![]() 上的值域為[-2,1]
上的值域為[-2,1]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() ,底面
,底面![]() 為菱形,
為菱形,![]() ,
,![]() 為
為![]() 上的點,過
上的點,過![]() 的平面分別交
的平面分別交![]() ,
,![]() 于點
于點![]() ,
,![]() ,且
,且![]() 平面
平面![]() .
.
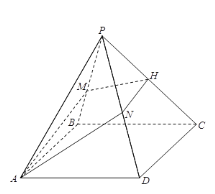
(1)證明:![]() ;
;
(2)當![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com