
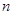 堆的第
堆的第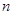 層就放一個乒乓球,以
層就放一個乒乓球,以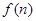 表示第
表示第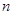 堆的乒乓球總數(shù).
堆的乒乓球總數(shù).


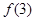 ;
;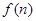 (用
(用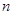 表示)(可能用到的公式:
表示)(可能用到的公式: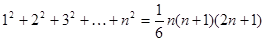 )
) 怎樣學(xué)好牛津英語系列答案
怎樣學(xué)好牛津英語系列答案 導(dǎo)學(xué)教程高中新課標系列答案
導(dǎo)學(xué)教程高中新課標系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
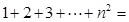
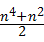 ,則當n=k+1時左端應(yīng)在n=k的基礎(chǔ)上增加 ( )
,則當n=k+1時左端應(yīng)在n=k的基礎(chǔ)上增加 ( ) | A.k2+1 |
| B.(k+1)2 |
C.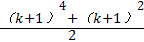 |
| D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
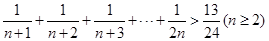 的過程中,
的過程中,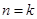 遞推到
遞推到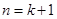 時的不等式左邊( )
時的不等式左邊( )A.增加了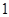 項 項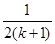 |
B.增加了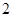 項 項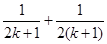 |
C.增加了“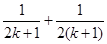 ”,又減少了“ ”,又減少了“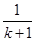 ” ” |
D.增加了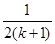 ,減少了“ ,減少了“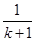 ” ” |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
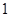 條線段,將圓分割成兩部分;畫
條線段,將圓分割成兩部分;畫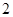 條相交線段,彼此分割成
條相交線段,彼此分割成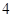 條線段,將圓分割成
條線段,將圓分割成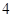 部分;畫
部分;畫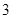 條線段,彼此最多分割成
條線段,彼此最多分割成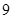 條線段,將圓最多分割成
條線段,將圓最多分割成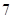 部分;畫
部分;畫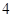 條線段,彼此最多分割成
條線段,彼此最多分割成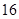 條線段,將圓最多分割成
條線段,將圓最多分割成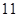 部分.
部分.


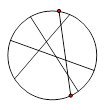
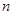 條線段,彼此最多分割成多少條線段?
條線段,彼此最多分割成多少條線段?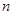 條線段,將圓最多分割成
條線段,將圓最多分割成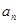 部分,歸納出
部分,歸納出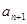 與
與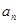 的關(guān)系.
的關(guān)系.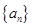 的通項公式,根據(jù)
的通項公式,根據(jù)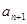 與
與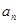 的關(guān)系及數(shù)列的知識,證明你的猜想是否成立.
的關(guān)系及數(shù)列的知識,證明你的猜想是否成立.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
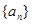 中,
中,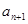 是函數(shù)
是函數(shù)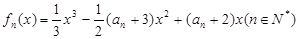 的極小值點,且
的極小值點,且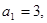
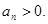
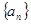 的通項公式;
的通項公式;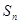 為數(shù)列
為數(shù)列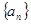 的前
的前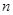 項和,試比較
項和,試比較 與
與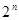 的大小關(guān)系.
的大小關(guān)系.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.n=1時成立 | B.n=2時成立 |
| C.n=3時成立 | D.n=4時成立 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com