
【題目】在平面直角坐標系中,動點![]() 到兩點
到兩點![]() 的距離之和等于4,設點
的距離之和等于4,設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 過點
過點![]() 且與曲線
且與曲線![]() 交于
交于![]() 兩點.
兩點.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)![]() 的面積是否存在最大值,若存在,求出
的面積是否存在最大值,若存在,求出![]() 的面積的最大值;若不存在,說明理由.
的面積的最大值;若不存在,說明理由.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的離心率e=
=1(a>b>0)的離心率e= ![]() ,右頂點、上頂點分別為A,B,直線AB被圓O:x2+y2=1截得的弦長為
,右頂點、上頂點分別為A,B,直線AB被圓O:x2+y2=1截得的弦長為 ![]()
(1)求橢圓C的方程;
(2)設過點B且斜率為k的動直線l與橢圓C的另一個交點為M, ![]() =λ(
=λ( ![]() ),若點N在圓O上,求正實數λ的取值范圍.
),若點N在圓O上,求正實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面內兩點A(4,0),B(0,2)
(1)求過P(2,3)點且與直線AB平行的直線l的方程;
(2)設O(0,0),求△OAB外接圓方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體是由以等邊三角形ABC為底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,AF=2,BD=1,CE=3,O為BC的中點.

(1)求證:面EFD⊥面BCED;
(2)求平面DEF與平面ACEF所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓的兩個焦點分別為![]() ,
, ![]() ,過
,過![]() 作橢圓長軸的垂線交橢圓于點
作橢圓長軸的垂線交橢圓于點![]() ,若
,若![]() 為等腰直角三角形,則橢圓的離心率是( )
為等腰直角三角形,則橢圓的離心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】試題分析:解:設點P在x軸上方,坐標為(![]() ),∵
),∵![]() 為等腰直角三角形,∴|PF2|=|F1F2|,
為等腰直角三角形,∴|PF2|=|F1F2|, ![]() ,故選D.
,故選D.
考點:橢圓的簡單性質
點評:本題主要考查了橢圓的簡單性質.橢圓的離心率是高考中選擇填空題常考的題目.應熟練掌握圓錐曲線中a,b,c和e的關系
【題型】單選題
【結束】
8
【題目】“![]() ”是“對任意的正數
”是“對任意的正數![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要條件 B. 必要不充分條件 C. 充要條件 D. 既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點![]() 到點
到點![]() ,
, ![]() 及到直線
及到直線![]() 的距離都相等,如果這樣的點恰好只有一個,那么實數
的距離都相等,如果這樣的點恰好只有一個,那么實數![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
【答案】D
【解析】試題分析:由題意知![]() 在拋物線
在拋物線![]() 上,設
上,設 ,則有
,則有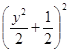
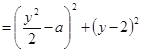 ,化簡得
,化簡得![]() ,當
,當![]() 時,符合題意;當
時,符合題意;當![]() 時,
時,![]() ,有
,有![]() ,
,![]() ,則
,則![]() ,所以選D.
,所以選D.
考點:1、點到直線的距離公式;2、拋物線的性質.
【方法點睛】本題考查拋物線的概念、性質以及數形結合思想,屬于中檔題,到點![]() 和直線
和直線![]() 的距離相等,則
的距離相等,則![]() 的軌跡是拋物線,再由直線與拋物線的位置關系可求;拋物線的定義是解決物線問題的基礎,它能將兩種距離(拋物線上的點到到焦點的距離、拋物線上的點到準線的距離)進行等量轉化,如果問題中涉及拋物線的焦點和準線,又能與距離聯系起來,那么用拋物線的定義就能解決.
的軌跡是拋物線,再由直線與拋物線的位置關系可求;拋物線的定義是解決物線問題的基礎,它能將兩種距離(拋物線上的點到到焦點的距離、拋物線上的點到準線的距離)進行等量轉化,如果問題中涉及拋物線的焦點和準線,又能與距離聯系起來,那么用拋物線的定義就能解決.
【題型】單選題
【結束】
13
【題目】在極坐標系中,已知兩點![]() ,
, ![]() ,則
,則![]() ,
, ![]() 兩點間的距離為__________.
兩點間的距離為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() 和點
和點![]() ,動圓
,動圓![]() 經過點
經過點![]() 且與圓
且與圓![]() 相切,圓心
相切,圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)點![]() 是曲線
是曲線![]() 與
與![]() 軸正半軸的交點,點
軸正半軸的交點,點![]() ,
, ![]() 在曲線
在曲線![]() 上,若直線
上,若直線![]() ,
, ![]() 的斜率分別是
的斜率分別是![]() ,
, ![]() ,滿足
,滿足![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農科所對冬季晝夜溫差大小與某反季節大豆新品種發芽多少之間的關系進行分析研究,他們分別記錄了12月1日至12月5日的晝夜溫差與實驗室每天每100顆種子中的發芽數,得到如下資料:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
溫差x(℃) | 10 | 11 | 13 | 12 | 8 |
發芽數y(顆) | 23 | 25 | 30 | 26 | 16 |
該農科所確定的研究方案是:先從這5組數據中選取2組,用剩下的3組數據求回歸方程,再對被選取的2組數據進行檢驗.
(1)求選取的2組數據恰好是不相鄰的2天數據的概率;
(2)若選取的是12月1日與12月5日的兩組數據,請根據12月2日至12月4日的數據,求y關于x的線性回歸方程![]()
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差不超過2顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得的線性回歸方程是否可靠?
(附:對于一組數據(x1,y1),(x2,y2),…,(xn,yn),其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為
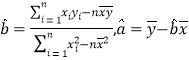
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com