定義:如果數列{an}的任意連續三項均能構成一個三角形的三邊長,則稱{an}為“三角形”數列.對于“三角形”數列{an},如果函數y=f(x)使得bn=f(an)仍為一個“三角形”數列,則稱y=f(x)是數列{an}的“保三角形函數”(n∈N*).
(Ⅰ)已知{an}是首項為2,公差為1的等差數列,若f(x)=kx(k>1)是數列{an}的“保三角形函數”,求k的取值范圍;
(Ⅱ)已知數列{cn}的首項為2013,Sn是數列{cn}的前n項和,且滿足4Sn+1-3Sn=8052,證明{cn}是“三角形”數列;
(Ⅲ)若g(x)=lgx是(Ⅱ)中數列{cn}的“保三角形函數”,問數列{cn}最多有多少項?
(解題中可用以下數據:lg2≈0.301,lg3≈0.477,lg2013≈3.304)
【答案】
分析:(Ⅰ)確定{a
n}是三角形數列,再利用函數的單調性,可得不等式,即可求k的取值范圍;
(Ⅱ)求得數列{c
n}的通項,再利用定義進行證明即可;
(Ⅲ)確定{g(c
n)}單調遞減,利用定義可得不等式

且lgc
n-1+lgc
n>lgc
n-2,由此可得n的范圍,從而可得結論.
解答:(Ⅰ)解:顯然a
n=n+1,a
n+a
n+1>a
n+2對任意正整數都成立,即{a
n}是三角形數列.
因為k>1,顯然有f(a
n)<f(a
n+1)<f(a
n+2)<…,
由f(a
n)+f(a
n+1)>f(a
n+2)得k
n+k
n+1>k
n+2解得

.
所以當
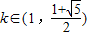
時,f(x)=k
x是數列{a
n}的保三角形函數.…(3分)
(Ⅱ)證明:由4s
n+1-3s
n=8052,得4s
n-3s
n-1=8052,
兩式相減得4c
n+1-3c
n=0,所以

…(5分)
經檢驗,此通項公式滿足4s
n+1-3s
n=8052.
顯然c
n>c
n+1>c
n+2,
因為

,
所以{c
n}是三角形數列.…(8分)
(Ⅲ)解:

,
所以{g(c
n)}單調遞減.
由題意知,
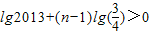
①且lgc
n-1+lgc
n>lgc
n-2②,
由①得
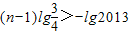
,解得n<27.4,
由②得

,解得n<26.4.
即數列{b
n}最多有26項.…(13分)
點評:本題考查新定義,考查函數的單調性,考查解不等式,考查學生分析解決問題的能力,正確理解新定義是關鍵.

 且lgcn-1+lgcn>lgcn-2,由此可得n的范圍,從而可得結論.
且lgcn-1+lgcn>lgcn-2,由此可得n的范圍,從而可得結論. .
.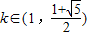 時,f(x)=kx是數列{an}的保三角形函數.…(3分)
時,f(x)=kx是數列{an}的保三角形函數.…(3分) …(5分)
…(5分) ,
, ,
,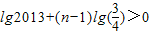 ①且lgcn-1+lgcn>lgcn-2②,
①且lgcn-1+lgcn>lgcn-2②,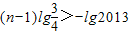 ,解得n<27.4,
,解得n<27.4, ,解得n<26.4.
,解得n<26.4.

 閱讀快車系列答案
閱讀快車系列答案