定義:如果數列{an}的任意連續三項均能構成一個三角形的三邊長,則稱{an}為“三角形”數列.對于“三角形”數列{an},如果函數y=f(x)使得bn=f(an)仍為一個“三角形”數列,則稱y=f(x)是數列{an}的“保三角形函數”,(n∈N﹡).
(1)已知{an}是首項為2,公差為1的等差數列,若f(x)=kx,(k>1)是數列{an}的“保三角形函數”,求k的取值范圍;
(2)已知數列{cn}的首項為2010,Sn是數列{cn}的前n項和,且滿足4Sn+1-3Sn=8040,證明{cn}是“三角形”數列;
(3)[文科]若g(x)=lgx是(2)中數列{cn}的“保三角形函數”,問數列{cn}最多有多少項.
[理科]根據“保三角形函數”的定義,對函數h(x)=-x2+2x,x∈[1,A],和數列1,1+d,1+2d,(d>0)提出一個正確的命題,并說明理由.
解:(1)顯然a
n=n+1,a
n+a
n+1>a
n+2對任意正整數都成立,
即{a
n}是三角形數列.(2分)
因為k>1,顯然有f(a
n)<f(a
n+1)<f(a
n+2),
由f(a
n)+f(a
n+1)>f(a
n+2)得k
n+k
n+1>k
n+2,解得k<

.
所以當k∈(1,

)時,f(x)=k
x是數列{a
n}的“保三角形函數”.(5分)
(2)由4S
n+1-3S
n=8040得4S
n-3S
n-1=8040,兩式相減得4c
n+1-3c
n=0
所以,c
n=2010
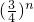
,
經檢驗,此通項公式滿足4S
n+1-3S
n=8040 (7分)
顯然c
n>c
n+1>c
n+2,因為c
n+1+c
n+2=2010
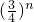
+2010
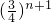
=•2010
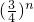
>c
n,
所以{c
n}是“三角形”數列.(10分)
(3)[文科]因為g(c
n)是單調遞減函數,所以,由lgc
n-1+lgc
n>lgc
n-2得
lg2010+(n-2)

lg+lg2010+(n-1)lg

>lg2010+(n-3)lg

(14分)
化簡得lg2010>nlg

,解得n<26.4,
即數列{b
n}最多有26項.(18分)
(3)[理科]探究過程:函數h(x)=-x
2+2x,x∈[1,A]是數列1,1+d,1+2d(d>0)的“保三角形函數”,必須滿足三個條件:
①1,1+d,1+2d(d>0)是三角形數列,所以1+1+d>1+2d,即o<d<1.
②數列中的各項必須在定義域內,即1+2d≤A.
③h(1),h(1+d),h(1+2d)是三角形數列.
由于h(x)=-x
2+2x,x∈[1,A]是單調遞減函數,所以h(1+d)+h(1+2d)>h(1),解得0<d<

.
分析:(1)先有條件得{a
n}是三角形數列,再利用f(x)=k
x,(k>1)是數列{a
n}的“保三角形函數”,得到k
n+k
n+1>k
n+2,解得k的取值范圍;
(2)先利用條件求出數列{c
n}的通項公式,再證明其滿足“三角形”數列的定義即可;
(3)[文科]利用條件得到g(c
n)是單調遞減函數以及lgc
n-1+lgc
n>lgc
n-2得,解此不等式找到對應的范圍即可得出結論.
[理科]根據函數h(x)=-x
2+2x,x∈[1,A]是數列1,1+d,1+2d(d>0)的“保三角形函數”,可以得到①1,1+d,1+2d(d>0)是三角形數列,所以1+1+d>1+2d,即o<d<1,②數列中的各項必須在定義域內,即1+2d≤A,③h(1),h(1+d),h(1+2d)是三角形數列;結論為在利用h(x)=-x
2+2x,x∈[1,A]是單調遞減函數,就可求出對應d的范圍.
點評:本題是在新定義下對數列的綜合考查.關于新定義的題型,在作題過程中一定要理解定義,并會用定義來解題.

 .
. )時,f(x)=kx是數列{an}的“保三角形函數”.(5分)
)時,f(x)=kx是數列{an}的“保三角形函數”.(5分)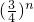 ,
,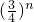 +2010
+2010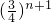 =•2010
=•2010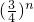 >cn,
>cn, lg+lg2010+(n-1)lg
lg+lg2010+(n-1)lg >lg2010+(n-3)lg
>lg2010+(n-3)lg (14分)
(14分) ,解得n<26.4,
,解得n<26.4, .
.
