Question

         如圖，在正三棱柱ABC—A₁B₁C₁中，點D是棱AB的中點，BC=1，AA₁=

   （1）求證：BC₁//平面A₁DC；

   （2）求二面角D—A₁C—A的大小

 

Answer 1

   （I）證明：連結AC₁交A₁C于點G，連結DG，

       在正三棱柱ABC—A₁B₁C₁中，四邊形ACC₁A₁是平行四邊形，

      

      

       …………2分

      

       …………4分

       （II）解法一： 過點D作交AC于E，過點D作交A₁C于F，

連結EF。

      

      

      

      

      

       是二面角D—A₁C—A的平面角，…………8分

       在直角三角形ADC中，

       同理可求：

       …………12分

       解法二：過點A作交BC于O，過點O作交B₁C₁于E。

因為平面

       所以，分別以CB、OE、OA所在的直線為建立空間直角坐標系，

如圖所示，因為是等邊三角形，所以O為BC的中點，則

   

…6分

   設平面A₁DC的法向量為

       則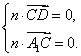

      

      

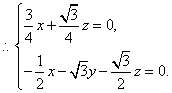
       取……8分

   可求平面ACA₁的一個法向量為…………10分

       設二面角D—A₁C—A的大小為

       …………12分