【答案】
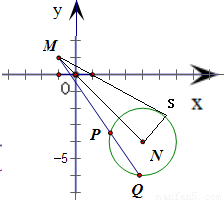
分析:根據(jù)向量的線性運(yùn)算,可得點(diǎn)N坐標(biāo)為(4,-4)且R點(diǎn)的軌跡是以N為圓心,半徑為2的圓.進(jìn)而得到P、Q在圓N上,且M、P、Q三點(diǎn)共線,在Rt△MNS中利用勾股定理,并結(jié)合圓的切割線定理即可算出
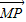
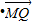
的值.
解答:解:∵
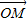
=(-1,1),
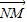
=(-5,5)
∴向量
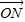
=
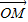
-
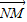
=(4,-4),即點(diǎn)N坐標(biāo)為(4,-4)
∵集合A={
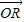
||
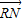
|=2}
∴點(diǎn)R到N的距離等于2(常數(shù)),故R點(diǎn)的軌跡是以N為圓心,半徑為2的圓
∵
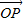
,
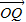
∈A且

=λ

(λ∈r,且λ≠0)
∴P、Q在圓N上,且M、P、Q三點(diǎn)共線
設(shè)過(guò)M的直線與圓N相切于點(diǎn)S,連接NS、NM,則
Rt△MNS中,MN=5
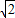
,NS=2,可得MS
2=MN
2-NS
2=50-4=46
由切割線定理,可得
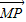
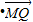
=
 2
2=46
故答案為:46
點(diǎn)評(píng):本題以向量為載體,求動(dòng)點(diǎn)的軌跡方程并求數(shù)量積
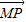
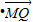
的值.著重考查了平面向量的線性運(yùn)算、平面向量數(shù)量積的運(yùn)算和動(dòng)點(diǎn)軌跡方程的求法等知識(shí),屬于中檔題.

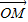 =(-1,1),
=(-1,1),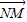 =(-5,5)集合A={
=(-5,5)集合A={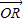 ||
||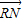 |=2},
|=2},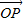 ,
,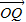 ∈A且
∈A且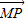 =λ
=λ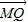 (λ∈r,且λ≠0)則
(λ∈r,且λ≠0)則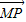
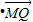 = .
= . 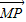
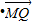 的值.
的值.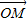 =(-1,1),
=(-1,1),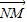 =(-5,5)
=(-5,5)
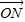 =
=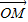 -
-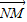 =(4,-4),即點(diǎn)N坐標(biāo)為(4,-4)
=(4,-4),即點(diǎn)N坐標(biāo)為(4,-4)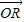 ||
||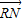 |=2}
|=2}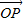 ,
,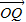 ∈A且
∈A且 =λ
=λ (λ∈r,且λ≠0)
(λ∈r,且λ≠0)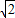 ,NS=2,可得MS2=MN2-NS2=50-4=46
,NS=2,可得MS2=MN2-NS2=50-4=46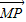
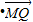 =
= 2=46
2=46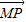
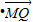 的值.著重考查了平面向量的線性運(yùn)算、平面向量數(shù)量積的運(yùn)算和動(dòng)點(diǎn)軌跡方程的求法等知識(shí),屬于中檔題.
的值.著重考查了平面向量的線性運(yùn)算、平面向量數(shù)量積的運(yùn)算和動(dòng)點(diǎn)軌跡方程的求法等知識(shí),屬于中檔題. 


 已知O為坐標(biāo)原點(diǎn),M(cosx,2
已知O為坐標(biāo)原點(diǎn),M(cosx,2