
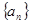 、
、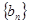 滿足
滿足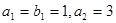 ,且
,且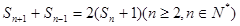 ,其中
,其中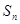 為數(shù)列
為數(shù)列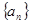 的前
的前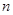 項(xiàng)和,又
項(xiàng)和,又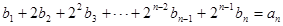 ,對任意
,對任意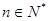 都成立。
都成立。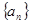 、
、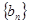 的通項(xiàng)公式;
的通項(xiàng)公式;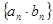 的前
的前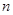 項(xiàng)和
項(xiàng)和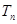
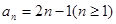 ,
,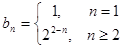 ;(2)
;(2)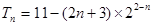 .
.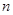 用
用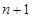 代替得到新的式子,兩式子作差,得出
代替得到新的式子,兩式子作差,得出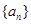 為等差數(shù)列,注意需檢驗(yàn)
為等差數(shù)列,注意需檢驗(yàn)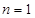 的情況,將
的情況,將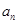 求出代入到已知的第2個(gè)式子中,用
求出代入到已知的第2個(gè)式子中,用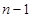 代替式子中的
代替式子中的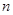 ,兩式子作差得到
,兩式子作差得到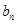 表達(dá)式;第二問,將
表達(dá)式;第二問,將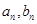 代入到
代入到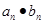 中,用錯(cuò)位相減法求和.
中,用錯(cuò)位相減法求和.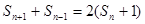 ,∴
,∴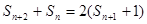
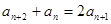
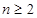 時(shí),數(shù)列
時(shí),數(shù)列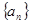 是等差數(shù)列,首項(xiàng)
是等差數(shù)列,首項(xiàng)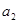 為3,公差為2,
為3,公差為2,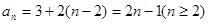 ,又
,又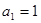 符合
符合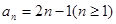 4分
4分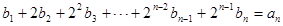 ,
,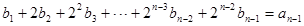
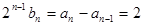 ,∴
,∴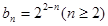
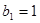 不滿足,∴
不滿足,∴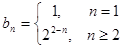 6分
6分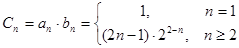
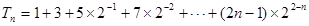
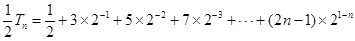
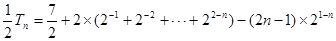
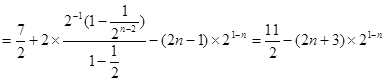
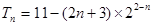 ..12分
..12分


| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
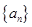 的通項(xiàng)公式為
的通項(xiàng)公式為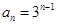 ,在等差數(shù)列數(shù)列
,在等差數(shù)列數(shù)列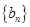 中,
中,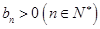 ,且
,且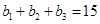 ,又
,又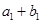 、
、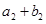 、
、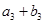 成等比數(shù)列.
成等比數(shù)列.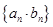 的通項(xiàng)公式;
的通項(xiàng)公式;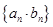 的前
的前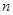 項(xiàng)和
項(xiàng)和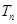 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
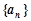 的前
的前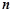 項(xiàng)和
項(xiàng)和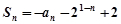 ,
,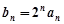 .
.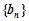 是等差數(shù)列;
是等差數(shù)列;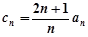 ,求數(shù)列
,求數(shù)列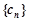 的前
的前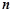 項(xiàng)和
項(xiàng)和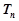 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
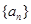 的前6項(xiàng)和為60,且
的前6項(xiàng)和為60,且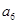 為
為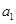 和
和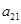 的等比中項(xiàng).
的等比中項(xiàng).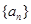 的通項(xiàng)公式;
的通項(xiàng)公式;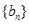 滿足
滿足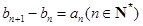 ,且
,且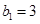 ,求數(shù)列
,求數(shù)列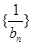 的前
的前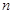 項(xiàng)和
項(xiàng)和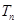 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
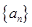 的前
的前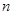 項(xiàng)和記為
項(xiàng)和記為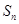 ,
,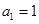 ,
,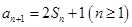 .
.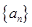 的通項(xiàng)公式;
的通項(xiàng)公式;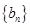 的前
的前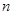 項(xiàng)和
項(xiàng)和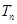 有最大值,且
有最大值,且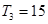 ,又
,又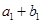 、
、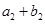 、
、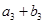 成等比數(shù)列,求
成等比數(shù)列,求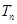 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
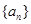 的首項(xiàng)
的首項(xiàng)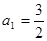 ,前n項(xiàng)和為Sn ,且滿足
,前n項(xiàng)和為Sn ,且滿足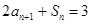 ( n∈N*) .則滿足
( n∈N*) .則滿足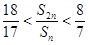 的所有n的和為 .
的所有n的和為 .查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com