
如圖,在四棱錐P-ABCD中,底面ABCD是平行四邊形,且 底面ABCD,
底面ABCD, ,E是PA的中點.
,E是PA的中點.

(1)求證:平面 平面EBD;
平面EBD;
(2)若PA=AB=2,求三棱錐P-EBD的高.
(1)證明過程詳見解析;(2)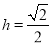 .
.
【解析】
試題分析:本題主要以四棱錐為幾何背景考查線面垂直、面面垂直、等體積法等基礎知識,考查空間想象能力、邏輯推理能力、計算能力.第一問,利用線面垂直的性質得PA⊥BD,又因為BD⊥PC,利用線面垂直的判定得到BD⊥平面PAC,最后利用面面垂直的判定得到平面PAC⊥平面EBD;第二問,由于BD⊥平面PAC,所以BD⊥AC,所以ABCD是菱形,可求出 的面積,由于BD⊥平面PAC,所以BD⊥OE,所以可求出
的面積,由于BD⊥平面PAC,所以BD⊥OE,所以可求出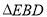 的面積,用等體積法求出三棱錐P-EBD的體積,通過列出的等式解出高的值.
的面積,用等體積法求出三棱錐P-EBD的體積,通過列出的等式解出高的值.
試題解析:(1)因為PA⊥平面ABCD,所以PA⊥BD.
又BD⊥PC,所以BD⊥平面PAC,
因為BD?平面EBD,所以平面PAC⊥平面EBD. 5分

(2)由(1)可知,BD⊥AC,所以ABCD是菱形,∠BAD=120?.
所以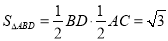 . 7分
. 7分
設AC∩BD=O,連結OE,則(1)可知,BD⊥OE.
所以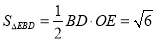 . 9分
. 9分
設三棱錐P-EBD的高為h,則
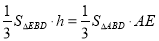 ,即
,即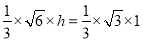 ,解得
,解得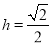 . 12分
. 12分
考點:線面垂直、面面垂直、等體積法.


科目:高中數學 來源:2013-2014學年河北省石家莊市畢業班第一次模擬考試數學理科數學試卷(解析版) 題型:解答題
已知數列{an}的各項均為正數的等比數列,且a1a2=2,a3a4=32,
(1)求數列{an}的通項公式;
(2)設數列{bn}滿足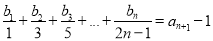 (n∈N*),求設數列{bn}的前n項和Tn.
(n∈N*),求設數列{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北省唐山市高三年級第二次模擬考試理科數學試卷(解析版) 題型:選擇題
將6名男生、4名女生分成兩組,每組5人,參加兩項不同的活動,每組3名男生和2名女生,則不同的分配方法有( )
A.240種 B.120種 C.60種 D.180種
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北省唐山市高三年級第二次模擬考試文科數學試卷(解析版) 題型:選擇題
用簡單隨機抽樣的方法從含有100個個體的總體中依次抽取一個容量為5的樣本,則個體m被抽到的概率為( )
A. B.
B.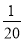 C.
C.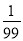 D.
D.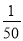
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北省高三下學期調研考試理科數學試卷(解析版) 題型:解答題
設函數
(1)若關于x的不等式 在
在 有實數解,求實數m的取值范圍;
有實數解,求實數m的取值范圍;
(2)設 ,若關于x的方程
,若關于x的方程 至少有一個解,求p的最小值.
至少有一個解,求p的最小值.
(3)證明不等式:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com