
【題目】某人上午7時乘船出發,以勻速![]() 海里/小時
海里/小時![]() 從
從![]() 港前往相距50海里的
港前往相距50海里的![]() 港,然后乘汽車以勻速
港,然后乘汽車以勻速![]() 千米/小時(
千米/小時(![]() )自
)自![]() 港前往相距
港前往相距![]() 千米的
千米的![]() 市,計劃當天下午4到9時到達
市,計劃當天下午4到9時到達![]() 市.設乘船和汽車的所要的時間分別為
市.設乘船和汽車的所要的時間分別為![]() 、
、![]() 小時,如果所需要的經費
小時,如果所需要的經費![]() (單位:元)
(單位:元)

(1)試用含有![]() 、
、![]() 的代數式表示
的代數式表示![]() ;
;
(2)要使得所需經費![]() 最少,求
最少,求![]() 和
和![]() 的值,并求出此時的費用.
的值,并求出此時的費用.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)分析題意,先用![]() 表示
表示![]() ,先用
,先用![]() 表示
表示![]() ,代入
,代入![]() ,化簡即可;(2)求出
,化簡即可;(2)求出![]() 滿足的約束條件,由約束條件畫出可行域,要求走得最經濟,即求可行域中的最優解,將目標函數看成是一條直線,分析目標函數
滿足的約束條件,由約束條件畫出可行域,要求走得最經濟,即求可行域中的最優解,將目標函數看成是一條直線,分析目標函數![]() 與直線截距的關系,進而求出最優.
與直線截距的關系,進而求出最優.
試題解析:(1) ![]() ,得
,得![]()
![]() ,得
,得![]()
![]()
所以![]() (其中
(其中![]() )
)
(2) ![]()
其中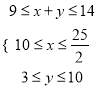 ,
,
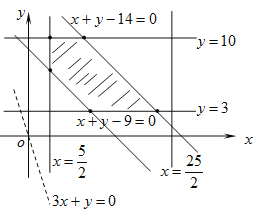
令目標函數![]() ,可行域的端點分別為
,可行域的端點分別為![]()
則當![]() 時,
時, ![]()
所以![]() (元),此時
(元),此時![]()
答:當![]() 時,所需要的費用最少,為
時,所需要的費用最少,為![]() 元.
元.
【方法點晴】本題主要考查線性規劃的應用及求目標函數的最值,屬簡單題.求目標函數最值的一般步驟是“一畫、二移、三求”:(1)作出可行域(一定要注意是實線還是虛線);(2)找到目標函數對應的最優解對應點(在可行域內平移變形后的目標函數,最先通過或最后通過的頂點就是最優解);(3)將最優解坐標代入目標函數求出最值.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案科目:高中數學 來源: 題型:
【題目】空氣質量主要受污染物排放量及大氣擴散等因素的影響,某市環保監測站2014年10月連續10天(從左到右對應1號至10號)采集該市某地平均風速及空氣中氧化物的日均濃度數據,制成散點圖如圖所示.
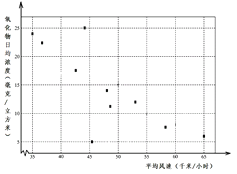
(Ⅰ)同學甲從這10天中隨機抽取連續5天的一組數據,計算回歸直線方程.試求連續5天的一組數據中恰好同時包含氧化物日均濃度最大與最小值的概率;
(Ⅱ)現有30名學生,每人任取5天數據,對應計算出30個不同的回歸直線方程.已知30組數據中有包含氧化物日均濃度最值的有14組.現采用這30個回歸方程對某一天平均風速下的氧化物日均濃度進行預測,若預測值與實測值差的絕對值小于2,則稱之為“擬合效果好”,否則為“擬合效果不好”.根據以上信息完成下列2×2聯表,并分析是否有95%以上的把握說擬合效果與選取數據是否包含氧化物日均濃度最值有關.
預測效果好 | 擬合效果不好 | 合計 | |
數據有包含最值 | 5 | ||
數據無包含最值 | 4 | ||
合計 |
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
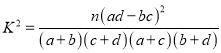 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin(2x+φ)(0<φ<2π)的圖象過點(![]() ,-2).
,-2).
(1)求φ的值;
(2)若f(![]() )=
)=![]() ,-
,-![]() <α<0,求sin(2α-
<α<0,求sin(2α-![]() )的值.
)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
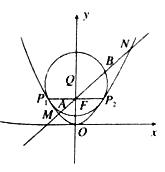
【題目】如圖,拋物線![]() 的準線為
的準線為![]() ,取過焦點
,取過焦點![]() 且平行于
且平行于![]() 軸的直線與拋物線交于不同的兩點
軸的直線與拋物線交于不同的兩點![]() ,過
,過![]() 作圓心為
作圓心為![]() 的圓,使拋物線上其余點均在圓外,且
的圓,使拋物線上其余點均在圓外,且![]() .
.
(Ⅰ)求拋物線![]() 和圓
和圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 作直線
作直線![]() 與拋物線
與拋物線![]() 和圓
和圓![]() 依次交于
依次交于![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分別是AP、AD的中點,求證: 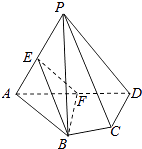
(1)直線EF∥平面PCD;
(2)平面BEF⊥平面PAD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐ABCD﹣PGFE中,底面ABCD是直角梯形,側棱垂直于底面,AB∥DC,∠ABC=45°,DC=1,AB=2,PA=1.
(Ⅰ)求PD與BC所成角的大小;
(Ⅱ)求證:BC⊥平面PAC;
(Ⅲ)求二面角A﹣PC﹣D的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com