
【題目】已知函數![]() .
.
(1)記![]() ,求證:函數
,求證:函數![]() 在區間
在區間![]() 內有且僅有一個零點;
內有且僅有一個零點;
(2)用![]() 表示
表示![]() 中的最小值,設函數
中的最小值,設函數![]() ,若關于
,若關于![]() 的方程
的方程![]() (其中
(其中![]() 為常數)在區間
為常數)在區間![]() 有兩個不相等的實根
有兩個不相等的實根![]() ,記
,記![]() 在
在![]() 內的零點為
內的零點為![]() ,試證明:
,試證明:![]() .
.
【答案】(1)證明見解析;(2)證明見解析.
【解析】
試題分析:(1)求出函數的導數,通過解關于導函數的不等式,得到函數的單調性,結合零點存在定理證出結論即可;(2)問題轉化為證明![]() ,根據
,根據![]() 在
在![]() 上遞減,即證明
上遞減,即證明![]() ,根據函數的單調性證明即可.
,根據函數的單調性證明即可.
試題解析:(1)證明:![]() ,
,
顯然當![]() 時,
時,![]() ,故
,故![]() 在
在![]() 上單調遞增,
上單調遞增,
而![]() ,所以由零點存在定理知,
,所以由零點存在定理知,
必存在唯一![]() ,使得
,使得![]() ,
,
即函數![]() 在區間
在區間![]() 內有且僅有一個零點.
內有且僅有一個零點.
(2)由(1)問可知![]() ,且
,且![]() 時,
時,![]() ,
,![]() 時
時![]() ,
,
因此![]() ,
,
其中![]() 滿足
滿足![]() 即
即![]() ,(事實上
,(事實上![]() ),
),
而![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
因此![]() 在
在![]() ,若方程
,若方程![]() 在區間
在區間![]() 有兩個不相等的實根,
有兩個不相等的實根,
![]() ,則必有
,則必有![]() ,
,
所證![]()
![]() ,因為
,因為![]() 在
在![]() 單調遞減,
單調遞減,
所以只需證![]() ,而
,而![]() ,所以只需證
,所以只需證![]() ,
,
即證明:![]() ,
,
構造函數![]() ,
,![]() ,
,
發現![]() ,
,![]() ,
,
下證明![]() 時,
時,![]() 恒成立,
恒成立,
考查函數![]() ,所以
,所以![]() 在
在![]() ,
,
所以一定有![]() ,
,
因此,![]() 時,
時,![]() ,
,
即![]() 在
在![]() ,所以
,所以![]() 時,
時,![]() 即成立了.
即成立了.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,矩形ABCD的一邊AB在x軸上,另一邊CD在x軸上方,且AB=8,BC=6,其中A(-4,0)、B(4,0)
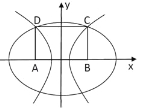
(1)若A、B為橢圓的焦點,且橢圓經過C、D兩點,求該橢圓的方程;
(2)若A、B為雙曲線的焦點,且雙曲線經過C、D兩點,求雙曲線的方程;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() .
.
(1)若直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
(2)若![]() 是直線
是直線![]() 上的動點,過
上的動點,過![]() 作圓
作圓![]() 的兩條切線
的兩條切線![]() ,切點為
,切點為![]() ,探究:直線
,探究:直線![]() 是否過定點;
是否過定點;
(3)若![]() 為圓
為圓![]() 的兩條相互垂直的弦,垂足為
的兩條相互垂直的弦,垂足為 ,求四邊形
,求四邊形![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
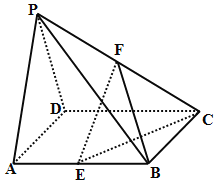
【題目】如圖所示,在四棱錐P-ABCD中,底面ABCD是棱長為2的正方形,側面PAD為正三角形,且面PAD⊥面ABCD,E、F分別為棱AB、PC的中點.
(1)求證:EF∥平面PAD;
(2)求三棱錐B-EFC的體積;
(3)求二面角P-EC-D的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校學生社團心理學研究小組在對學生上課注意力集中情況的調查研究中,發現其在40分鐘的一節課中,注意力指數![]() 與聽課時間
與聽課時間![]() (單位:分鐘)之間的關系滿足如圖所示的曲線.當
(單位:分鐘)之間的關系滿足如圖所示的曲線.當![]() 時,曲線是二次函數圖象的一部分,當
時,曲線是二次函數圖象的一部分,當![]() 時,曲線是函數
時,曲線是函數![]() 圖象的一部分.根據專家研究,當注意力指數
圖象的一部分.根據專家研究,當注意力指數![]() 大于80時學習效果最佳.
大于80時學習效果最佳.
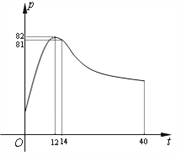
(1)試求![]() 的函數關系式;
的函數關系式;
(2)教師在什么時段內安排核心內容,能使得學生學習效果最佳?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地為制定初中七、八、九年級學生校服的生產計劃,有關部門準備對180名初中男生的身高作調查.
(1)為了達到估計該地初中三個年級男生身高分布的目的,你認為采用怎樣的調查方案比較合理?
(2)表中的數據是使用了某種調查方法獲得的:七、八、九年級180名男生身高:
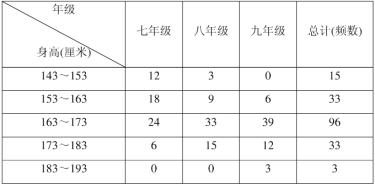
注:表中每組可含最低值,不含最高值.
根據表中的數據,請你給校服生產廠家指定一份生產計劃思路.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如下圖,已知四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.
的中點.

(I)證明:![]() 平面
平面![]() ;
;
(II)取![]() ,在線段
,在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 與平面
與平面![]() 所成最大角的正切值為
所成最大角的正切值為![]() ,若存在,請求出
,若存在,請求出![]() 點的位置;若不存在,請說明理由.
點的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com