
【題目】甲廠根據以往的生產銷售經驗得到下面有關生產銷售的關系:廠里的固定成本為2.8萬元,每生產1百臺的生產成本為1萬元,每生產產品x(百臺),其總成本為G(x)(萬元)(總成本=固定成本+生產成本).如果銷售收入R(x)= ![]() ,且該產品產銷平衡(即生產的產品都能賣掉),請完成下列問題:
,且該產品產銷平衡(即生產的產品都能賣掉),請完成下列問題:
(1)寫出利潤函數y=f(x)的解析式(利潤=銷售收入﹣總成本);
(2)甲廠生產多少臺新產品時,可使盈利最多?
【答案】
(1)解:由題意得G(x)=2.8+x.
∴f(x)=R(x)﹣G(x)= ![]()
(2)解:當x>5時,∵函數f(x)遞減,∴f(x)<=3.2(萬元).
當0≤x≤5時,函數f(x)=﹣0.4(x﹣4)2+3.6,
當x=4時,f(x)有最大值為3.6(萬元).
答:當工廠生產4百臺時,可使贏利最大為3.6萬元
【解析】(1)由題意得G(x)=2.8+x.由R(x)= ![]() ,f(x)=R(x)﹣G(x),能寫出利潤函數y=f(x)的解析式.(2)當x>5時,由函數f(x)遞減,知f(x)<f(5)=3.2(萬元).當0≤x≤5時,函數f(x)=﹣0.4(x﹣4)2+3.6,當x=4時,f(x)有最大值為3.6(萬元).由此能求出工廠生產多少臺產品時,可使盈利最多.
,f(x)=R(x)﹣G(x),能寫出利潤函數y=f(x)的解析式.(2)當x>5時,由函數f(x)遞減,知f(x)<f(5)=3.2(萬元).當0≤x≤5時,函數f(x)=﹣0.4(x﹣4)2+3.6,當x=4時,f(x)有最大值為3.6(萬元).由此能求出工廠生產多少臺產品時,可使盈利最多.


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為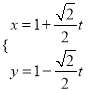 (
(![]() 為參數),在極坐標系(與直角坐標系
為參數),在極坐標系(與直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的極坐標方程為
的極坐標方程為![]() ,圓
,圓![]() 與直線
與直線![]() 交于
交于![]() ,
, ![]() 兩點,
兩點, ![]() 點的直角坐標為
點的直角坐標為![]() .
.
(Ⅰ)將直線![]() 的參數方程化為普通方程,圓
的參數方程化為普通方程,圓![]() 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
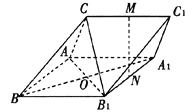
【題目】如圖,三棱柱ABC-A1B1Cl中,M,N分別為CC1,A1B1的中點.
(I)證明:直線MN//平面CAB1;
(II)BA=BC=BB1,CA=CB1,CA⊥CB1,∠ABB1=60°,求平面AB1C和平面A1B1C1所成的角(銳角)的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知⊙![]() :
: ![]() 與⊙
與⊙![]() :
: ![]() ,以
,以![]() ,
, ![]() 分別為左右焦點的橢圓
分別為左右焦點的橢圓![]() :
: ![]() 經過兩圓的交點。
經過兩圓的交點。
(Ⅰ)求橢圓![]() 的方程;
的方程;
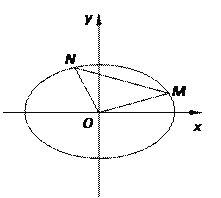
(Ⅱ)![]() 、
、![]() 是橢圓
是橢圓![]() 上的兩點,若直線
上的兩點,若直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,試問
,試問![]() 的面積是否為定值?若是,求出這個定值;若不是,請說明理由。
的面積是否為定值?若是,求出這個定值;若不是,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|﹣1≤x≤10},集合B={x|2x﹣6≥0}.
求R(A∪B);
已知C={x|a<x<a+1},且CA,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,點 ![]() 的極坐標是
的極坐標是![]() ,曲線
,曲線 ![]() 的極坐標方程為
的極坐標方程為![]() .以極點為坐標原點,極軸為
.以極點為坐標原點,極軸為 ![]() 軸的正半軸建立平面直角坐標系,斜率為
軸的正半軸建立平面直角坐標系,斜率為 ![]() 的直線
的直線 ![]() 經過點
經過點![]() .
.
(1)寫出直線 ![]() 的參數方程和曲線
的參數方程和曲線 ![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線 ![]() 和曲線
和曲線![]() 相交于兩點
相交于兩點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com