【題目】設函數
．
（1）當
時，求函數
在點
處的切線方程；
（2）討論函數
的單調性；
（3）當
時，求證：對任意
，都有
．
【答案】（1）
；（2）見解析；（3）見解析.
【解析】試題分析：（1）當
時，求出導數易得
，即
，利用點斜式可得其切線方程；（2）求得可得
，分為
和
兩種情形判斷其單調性；（3）當
時，根據（2）可得函數
在
上單調遞減，故
，即
，化簡可得所證結論.
試題解析：（1）當
時， 
， 
， 
， 
，所以函數
在點
處的切線方程為
，即
．
（2）
，定義域為
， 
．
① 當
時， 
，故函數
在
上單調遞減；
② 當
時，令
，得
x |
|
|
|
|
|
|
|
| ↘ | 極小值 | ↗ |
綜上所述，當
時， 
在
上單調遞減；當
時，函數
在
上單調遞減，在
上單調遞增．
（3）當
時，由（2）可知，函數
在
上單調遞減，顯然， 
，故
，所以函數
在
上單調遞減，對任意
，都有
，所以
．所以
，即
，所以
，即
，所以
，即
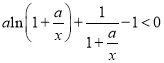，所以
．
科目：高中數學 來源： 題型：
【題目】如圖，已知矩形ABCD所在平面外一點P，PA⊥平面ABCD，E、F分別是AB，PC的中點．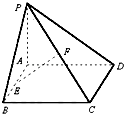 
（1）求證：EF∥平面PAD；
（2）求證：EF⊥CD；
（3）若∠PDA=45°，求EF與平面ABCD所成的角的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方形O′A′B′C′的邊長為1cm，它是水平放置的一個平面圖形的直觀圖，則原圖的周長是（ ） 
A.8cm
B.6cm
C.2（1+ 
）cm
D.2（1+ 
）cm
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據下列條件，分別求直線方程：
（1）經過點A（3，0）且與直線2x+y﹣5=0垂直；
（2）求經過直線x﹣y﹣1=0與2x+y﹣2=0的交點，且平行于直線x+2y﹣3=0的直線方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有甲、乙兩種商品，經銷這兩種商品所能獲得的利潤分別是p萬元和q萬元．它們與投入資金x萬元的關系是：p= 
x，q= 
．今有3萬元資金投入經營這兩種商品，為獲得最大利潤，對這兩種商品的資金分別投入多少時，能獲取最大利潤？最大利潤為多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax2+lnx（a∈R）．
（1）當a=
時，求f（x）在區間[1，e]上的最大值和最小值；
（2）如果函數g（x），f1（x），f2（x），在公共定義域D上，滿足f1（x）＜g（x）＜f2（x），那么就稱g（x）為f1（x），f2（x）的“活動函數”．已知函數
. 
。若在區間（1，+∞）上，函數f（x）是f1（x），f2（x）的“活動函數”，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設集合A={x|2﹣5≤2﹣x≤4}，B={x|x2+2mx﹣3m2＜0，m＞0}．
（1）若m=2，求A∩B；
（2）若BA，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=cos（ωx+φ）（ω＞0），x=﹣ 
是y=f（x）的零點，直線x= 
為y=f（x）圖象的一條對稱軸，且函數f（x）在區間（ 
， 
）上單調，則ω的最大值是（ ）
A.9
B.7
C.5
D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
