
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)對![]() ,
,![]() 恒成立,求實數(shù)a的取值范圍;
恒成立,求實數(shù)a的取值范圍;
(2)當(dāng)![]() 時,求
時,求![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(3)證明:對![]() 都有
都有![]() 成立.
成立.
【答案】(1)![]() ;(2)詳見解析;(3)詳見解析.
;(2)詳見解析;(3)詳見解析.
【解析】
(1)原不等式等價于![]() ,參變分離可求參數(shù)
,參變分離可求參數(shù)![]() 的取值范圍.
的取值范圍.
(2)當(dāng)![]() 時,
時,![]() ,該函數(shù)的極小值點為
,該函數(shù)的極小值點為![]() ,因函數(shù)的定義域為
,因函數(shù)的定義域為![]() ,故分
,故分![]() 和
和![]() 兩種情況分類討論即可.
兩種情況分類討論即可.
(3)即證![]() 在
在![]() 上恒成立,也就是
上恒成立,也就是![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,
,![]() ,利用導(dǎo)數(shù)可證
,利用導(dǎo)數(shù)可證![]() .
.
(1)由題意![]() ,在
,在![]() 恒成立,
恒成立,
即![]() ,
,![]() ,在
,在![]() 恒成立,
恒成立,
設(shè)![]() ,只須
,只須![]() .
.
由于![]()
所以![]() 時,
時,![]() ,
,![]() 單調(diào)遞減;
單調(diào)遞減;
![]() 時,
時,![]() ,
,![]() 單調(diào)遞增;
單調(diào)遞增;
故![]() .因此
.因此![]() .
.
所以![]() 的取值范圍為
的取值范圍為![]() .
.
(2)![]() 時,
時,![]() ,
,![]() ,令
,令![]() ,得
,得![]() .
.
當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞減;
單調(diào)遞減;
![]() 時,
時,![]() ,
,![]() 單調(diào)遞增.
單調(diào)遞增.
故![]() 在
在![]() 時,
時,![]() 為最小值點,且
為最小值點,且![]() .
.
由題意![]() ,
,![]() ,
,
1°當(dāng)![]() 時,
時,![]() 在
在![]() 最小值為
最小值為![]() ,
,
![]() ,
,
由于![]() .
.
![]() .
.
故![]() .
.
即當(dāng)![]() 時,
時,![]() 在
在![]() 最小值為
最小值為![]() ,
,
最大值為![]() .
.
2°當(dāng)![]() 時,
時,![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
![]() ,
,
![]() ,
,
綜上所求![]() .
.
當(dāng)![]() 時,
時,![]() ,
,
當(dāng)![]() 時,
時,![]() .
.
(Ⅲ)即證:![]() ,
,
即證:![]() ,亦即證:
,亦即證:![]() ,
,
設(shè)![]() ,即
,即![]() ,
,
令![]() ,
,![]() ,
,
當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞減;
單調(diào)遞減;
當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞增.
單調(diào)遞增.
即![]() .
.
又設(shè)![]() ,
,![]() .
.
當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞增;
單調(diào)遞增;
當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞減.
單調(diào)遞減.
故![]() .
.
所以![]() 最小值與
最小值與![]() 最大值均為
最大值均為![]() .
.
但![]() 取得最小值與
取得最小值與![]() 取得最大值時的
取得最大值時的![]() 不相同,故,
不相同,故,
即![]() 成立,亦即結(jié)論成立.
成立,亦即結(jié)論成立.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() 、
、![]() 為雙曲線
為雙曲線![]()
![]() 的左、右焦點,過
的左、右焦點,過![]() 作垂直于
作垂直于![]() 軸的直線,在
軸的直線,在![]() 軸上方交雙曲線
軸上方交雙曲線![]() 于點
于點![]() ,且
,且![]() ,圓
,圓![]() 的方程是
的方程是![]() .
.
(1)求雙曲線![]() 的方程;
的方程;
(2)過雙曲線![]() 上任意一點
上任意一點![]() 作該雙曲線兩條漸近線的垂線,垂足分別為
作該雙曲線兩條漸近線的垂線,垂足分別為![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)過圓![]() 上任意一點
上任意一點![]() 作圓
作圓![]() 的切線
的切線![]() 交雙曲線
交雙曲線![]() 于
于![]() 、
、![]() 兩點,
兩點,![]() 中點為
中點為![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
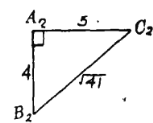
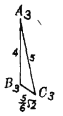
【題目】現(xiàn)有邊長分別3,4,5的三角形兩個,邊長分別4,5,![]() 的三角形四個,邊長分別為
的三角形四個,邊長分別為![]() ,4,5的三角形六個.用上述三角形為面,可以拼成______個四面體.
,4,5的三角形六個.用上述三角形為面,可以拼成______個四面體.
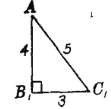
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出以下關(guān)于線性方程組解的個數(shù)的命題.
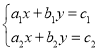 ①,
①,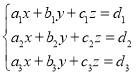 ②,
②,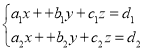 ③,
③, ④,
④,
(1)方程組①可能有無窮多組解;
(2)方程組②可能有且只有兩組不同的解;
(3)方程組③可能有且只有唯一一組解;
(4)方程組④可能有且只有唯一一組解.
其中真命題的序號為________________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .其中
.其中![]() 表示
表示![]() 的導(dǎo)函數(shù)
的導(dǎo)函數(shù)![]() 在
在![]() 的取值.
的取值.
(1)求![]() 的值及函數(shù)
的值及函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() 在
在![]() 的定義域內(nèi)恒成立,求
的定義域內(nèi)恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在數(shù)列![]() 中,已知
中,已知![]() ,對于任意的
,對于任意的![]() ,有
,有![]() .
.
(1)求數(shù)列![]() 的通項公式.
的通項公式.
(2)若數(shù)列![]() 滿足
滿足![]() ,求數(shù)列
,求數(shù)列![]() 的通項公式.
的通項公式.
(3)設(shè)![]() ,是否存在實數(shù)
,是否存在實數(shù)![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() 恒成立?若存在,求實數(shù)
恒成立?若存在,求實數(shù)![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求該函數(shù)的定義域;
時,求該函數(shù)的定義域;
(2)當(dāng)![]() 時,如果
時,如果![]() 對任何
對任何![]() 都成立,求實數(shù)
都成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,將函數(shù)
,將函數(shù)![]() 的圖像沿
的圖像沿![]() 軸方向平移,得到一個偶函數(shù)
軸方向平移,得到一個偶函數(shù)![]() 的圖像,設(shè)函數(shù)
的圖像,設(shè)函數(shù)![]() 的最大值為
的最大值為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若數(shù)列![]() 同時滿足:①對于任意的正整數(shù)
同時滿足:①對于任意的正整數(shù)![]() ,
, ![]() 恒成立;②對于給定的正整數(shù)
恒成立;②對于給定的正整數(shù)![]() ,
, ![]() 對于任意的正整數(shù)
對于任意的正整數(shù)![]() 恒成立,則稱數(shù)列
恒成立,則稱數(shù)列![]() 是“
是“![]() 數(shù)列”.
數(shù)列”.
(1)已知![]() 判斷數(shù)列
判斷數(shù)列![]() 是否為“
是否為“![]() 數(shù)列”,并說明理由;
數(shù)列”,并說明理由;
(2)已知數(shù)列![]() 是“
是“![]() 數(shù)列”,且存在整數(shù)
數(shù)列”,且存在整數(shù)![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差數(shù)列,證明:
成等差數(shù)列,證明: ![]() 是等差數(shù)列.
是等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)在高二下學(xué)期開設(shè)四門數(shù)學(xué)選修課,分別為《數(shù)學(xué)史選講》.《球面上的幾何》.《對稱與群》.《矩陣與變換》.現(xiàn)有甲.乙.丙.丁四位同學(xué)從這四門選修課程中選修一門,且這四位同學(xué)選修的課程互不相同,下面關(guān)于他們選課的一些信息:①甲同學(xué)和丙同學(xué)均不選《球面上的幾何》,也不選《對稱與群》:②乙同學(xué)不選《對稱與群》,也不選《數(shù)學(xué)史選講》:③如果甲同學(xué)不選《數(shù)學(xué)史選講》,那么丁同學(xué)就不選《對稱與群》.若這些信息都是正確的,則丙同學(xué)選修的課程是( )
A. 《數(shù)學(xué)史選講》B. 《球面上的幾何》C. 《對稱與群》D. 《矩陣與變換》
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com