
分析 先根據定積分的幾何意義,將原式化成${∫}_{0}^{1}$(1-x2)dx+${∫}_{1}^{3}$(x2-1)dx,再利用定積分的運算法則,找出被積函數的原函數,進行計算即可.
解答 解:由題意可知:$\int_{0}^{3}{|{x^2}-1|}dx$=${∫}_{0}^{1}$(1-x2)dx+${∫}_{1}^{3}$(x2-1)dx,
=(x-$\frac{1}{3}$x3)${丨}_{0}^{1}$+($\frac{1}{3}$x3-x)${丨}_{1}^{3}$,
=(1-$\frac{1}{3}$)+(9-3)+($\frac{1}{3}$-1),
=$\frac{22}{3}$,
故答案為:$\frac{22}{3}$.
點評 本題主要考查定積分的基本運算,解題關鍵是找出被積函數的原函數,利用區間去絕對值符號也是注意點,屬于基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
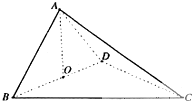 如圖,四面體ABCD中,O是BD的中點,△ABD和△BCD均為等邊三角形,AB=2,AC=$\sqrt{6}$.
如圖,四面體ABCD中,O是BD的中點,△ABD和△BCD均為等邊三角形,AB=2,AC=$\sqrt{6}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com