
(1)已知函數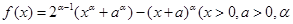 為有理數且
為有理數且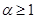 ),求函數
),求函數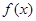 的最小值;
的最小值;
(2)①試用(1)的結果證明命題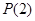 :設
:設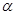 為有理數且
為有理數且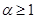 ,若
,若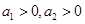 時,則
時,則 ;
;
②請將命題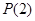 推廣到一般形式
推廣到一般形式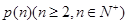 ,并證明你的結論;
,并證明你的結論;
注:當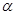 為正有理數時,有求導公式
為正有理數時,有求導公式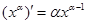
(1)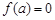 (2)①關鍵是利用函數的最小值為
(2)①關鍵是利用函數的最小值為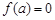 ②利用數學歸納法可證。
②利用數學歸納法可證。
【解析】
試題分析:解:(Ⅰ)令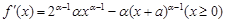
得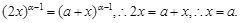
當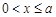 時,
時,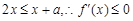 ,故
,故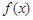 在
在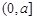 上遞減.
上遞減.
當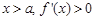 ,故
,故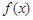 在
在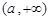 上遞增.
上遞增.
所以,當 時,
時,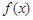 的最小值為
的最小值為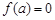
(Ⅱ)(ⅰ)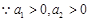 ,令
,令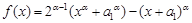 ,由(Ⅰ)知
,由(Ⅰ)知
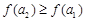 ,
,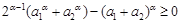 ,即
,即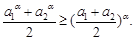
(ⅱ)命題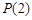 推廣到一般形式
推廣到一般形式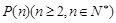 為:設
為:設 為有理數且
為有理數且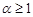 ,
,
若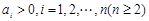 時,則
時,則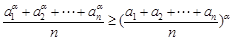 .
.
下面用數學歸納法證明如下:①當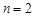 時,由(Ⅱ)(ⅰ)知,不等式成立;
時,由(Ⅱ)(ⅰ)知,不等式成立;
②假設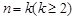 時,不等式成立,即
時,不等式成立,即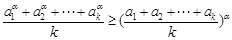 ,
,
那么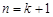 時,要證
時,要證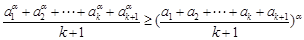 ,
,
即證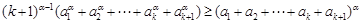 ,
,
設函數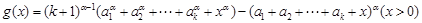 ,
,
則 ,
,
令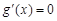 ,得
,得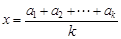 ,
,
當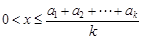 時,
時,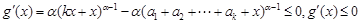 ,
,
故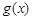 在
在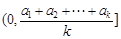 上遞減;
上遞減;
當 ,類似可證
,類似可證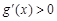 ,故
,故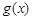 在
在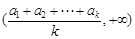 上遞增.
上遞增.
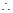 當
當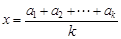 時,
時,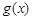 的最小值為
的最小值為
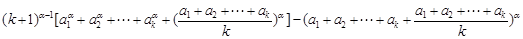
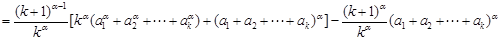
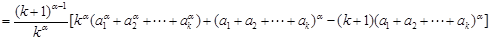
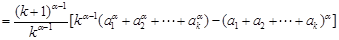 ,
,
由歸納假設知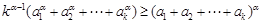 ,所以
,所以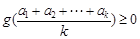 ,
,
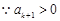 ,
,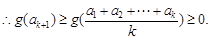
 時不等式成立.
時不等式成立.
綜上,原命題得證
考點:數學歸納法
點評:本題用到的數學歸納法,在高中數學中常用來證明等式成立和數列通項公式成立。若要證明一個與自然數n有關的命題P(n),有如下步驟:
(1)證明當n取第一個值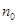 時命題成立。
時命題成立。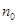 對于一般數列取值為0或1,但也有特殊情況;
對于一般數列取值為0或1,但也有特殊情況;
(2)假設當n=k(k≥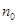 ,k為自然數)時命題成立,證明當n=k+1時命題也成立。
,k為自然數)時命題成立,證明當n=k+1時命題也成立。
綜合(1)(2),對一切自然數n(≥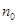 ),命題P(n)都成立。
),命題P(n)都成立。


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案科目:高中數學 來源: 題型:
|
| A、1個 | B、2個 | C、3個 | D、4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
 ,給出下列關于f(x)的性質:
,給出下列關于f(x)的性質:查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
|
| A.1個 | B.2個 | C.3個 | D.4個 |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京五中高三(上)第二次月考數學試卷(理科)(解析版) 題型:選擇題
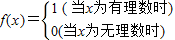 ,給出下列關于f(x)的性質:
,給出下列關于f(x)的性質:查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京五中高三(上)第二次月考數學試卷(文科)(解析版) 題型:選擇題
 ,給出下列關于f(x)的性質:
,給出下列關于f(x)的性質:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com