
【題目】已知函數![]() .
.
(Ⅰ)若函數![]() 在
在![]() 上是減函數,求實數
上是減函數,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)當![]() 時,求證:對任意
時,求證:對任意![]() ,函數
,函數![]() 的圖象均在
的圖象均在![]() 軸上方.
軸上方.
【答案】(Ⅰ)![]() (Ⅱ)見解析
(Ⅱ)見解析
【解析】
(Ⅰ)根據已知條件將問題轉化為![]() 恒成立,進而轉化為求函數
恒成立,進而轉化為求函數![]() 的最值即可求解;
的最值即可求解;
(Ⅱ)將不等式恒成立問題運用分離參數法,轉化為函數的最值問題,即可得證.
(Ⅰ)根據題意,得![]() (
(![]() ).因為函數
).因為函數![]() 在
在![]() 上是減函數,
上是減函數,
所以![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 恒成立,
恒成立,
故只需![]() (
(![]() ).
).
令函數![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,所以
,所以![]() ,解得
,解得![]() ;
;
所以實數![]() 的取值范圍是
的取值范圍是![]() .
.
(Ⅱ)當![]() 時,函數
時,函數![]() (
(![]() ),則
),則![]() .
.
令函數![]() ,則
,則![]() .因為
.因為![]() ,
,
所以函數![]() 在
在![]() 上單調遞增.
上單調遞增.
又因為![]() ,
,![]() ,
,
所以存在![]() ,使
,使![]() ,可得
,可得![]() ,
,
所以對任意![]() ,
,![]() ,即
,即![]() ,函數
,函數![]() 在
在![]() 上單調遞減;
上單調遞減;
對任意![]() ,
,![]() ,即
,即![]() ,函數
,函數![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() .
.
要證函數![]() 的圖象均在
的圖象均在![]() 軸上方,只需證
軸上方,只需證![]() ,
,
即當![]() 時,
時,![]() 恒成立,
恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
因為當![]() 時,函數
時,函數![]() 是減函數,所以
是減函數,所以![]() ,
,
則![]() ,解得
,解得![]() ,
,
所以當![]() 時,對任意
時,對任意![]() ,函數
,函數![]() 的圖象均在
的圖象均在![]() 軸上方.
軸上方.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:
【題目】某調查機構對某校學生做了一個是否同意生“二孩”抽樣調查,該調查機構從該校隨機抽查了100名不同性別的學生,調查統計他們是同意父母生“二孩”還是反對父母生“二孩”,現已得知100人中同意父母生“二孩”占60%,統計情況如下表:
同意 | 不同意 | 合計 | |
男生 | a | 5 | |
女生 | 40 | d | |
合計 | 100 |
(1)求 a,d 的值,根據以上數據,能否有97.5%的把握認為是否同意父母生“二孩”與性別有關?請說明理由;
(2)將上述調查所得的頻率視為概率,現在從所有學生中,采用隨機抽樣的方法抽取4 位學生進行長期跟蹤調查,記被抽取的4位學生中持“同意”態度的人數為 X,求 X 的分布列及數學期望.
附: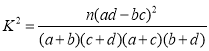
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近幾年,在國家大力支持和引導下,中國遙感衛星在社會生產和生活各領域的應用范圍不斷擴大,中國人民用遙感衛星系統研制工作取得了顯著成績,逐步形成了氣象、海洋、陸地資源和科學試驗等遙感衛星系統.如圖是2007—2018年中國衛星導航與位置服務產業總體產值規模(萬億)及增速(%)的統計圖,則下列結論中錯誤的是( )
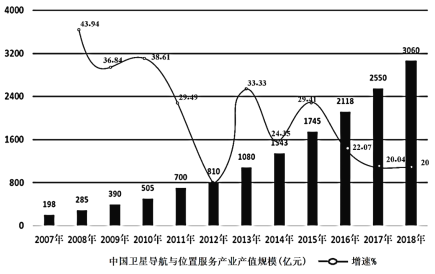
A.2017年中國衛星導航與位置服務產業總體產值規模達到2550億元,較2016年增長20.40%
B.若2019年中國衛星導航與位置服務產業總體產值規模保持2018年的增速,總體產值規模將達3672億元
C.2007—2018年中國衛星導航與位置服務產業總體產值規模逐年增加,但不與時間成正相關
D.2007—2018年中國衛星導航與位置服務產業總體產值規模的增速中有些與時間成負相關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某房地產開發商有一塊如圖(1)所示的四邊形空地ABCD,經測量,邊界CB與CD的長都為2km,所形成的角∠![]() .
.
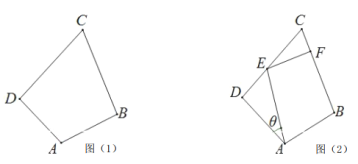
(I)如果邊界AD與AB所形成的角![]() ,現欲將該地塊用固定高度的板材圍成一個封閉的施工場地,求至多購買多少千米長度的板材;
,現欲將該地塊用固定高度的板材圍成一個封閉的施工場地,求至多購買多少千米長度的板材;
(II)當邊界AD與CD垂直,AB與BC垂直時,為后期開發方便,擬在這塊空地上先建兩條內部道路AE,EF,如圖(2)所示,點E在邊界CD上,且道路EF與邊界BC互相垂直,垂足為F,為節約成本,欲將道路AE,EF分別建成水泥路、砂石路,每1km的建設費用分別為![]() 、a元(a為常數);若設
、a元(a為常數);若設![]() ,試用
,試用![]() 表示道路AE,EF建設的總費用
表示道路AE,EF建設的總費用![]() (單位:元),并求出總費用
(單位:元),并求出總費用![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,(
,(![]() ).
).
(1)若曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,求實數a、m的值;
,求實數a、m的值;
(2)若![]() 對任意
對任意![]() 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍;
(3)關于x的方程![]() 能否有三個不同的實根?證明你的結論.
能否有三個不同的實根?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以直角坐標系的原點
為參數).以直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立坐標系,曲線
軸的正半軸為極軸建立坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)若過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,與
兩點,與![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com