
已知偶函數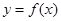 在區間
在區間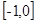 上是增函數,且滿足
上是增函數,且滿足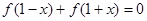 ,下列判斷中錯誤的是( )
,下列判斷中錯誤的是( )
A.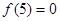
B.函數 在
在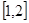 上單調遞減
上單調遞減
C.函數 的圖像關于直線
的圖像關于直線 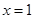 對稱
對稱
D.函數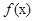 的周期是
的周期是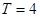
A
【解析】
試題分析:對于A,令x=0代入題中等式,得f(1-0)+f(1+0)=0,∴f(1)=0,結合函數為偶函數得f(-1)=f(1)=0,再令x=2代入題中等式,,得f(1-2)+f(1+2)=0,得f(3)=-f(-1)=0,結合函數為偶函數得f(-3)=f(3)=0,最后令x=4,f(1-4)+f(1+4)=0,得f(5)=-f(-3)=0,故A項正確;對于B,因為偶函數y=f(x)圖象關于y軸對稱,在區間[-1,0]上是增函數,所以y=f(x)在區間[0,1]上是減函數,設F(x)=f(1+x),得F(-x)=f(1-x),因為f(1-x)+f(1+x)=0,得f(1+x)=-f(1-x),所以F(x)=f(1+x)是奇函數,圖象關于原點對稱.由此可得y=f(x)圖象關于點(1,0)對稱.∵區間[1,2]和區間[0,1]是關于點(1,0)對稱的區間,且在對稱的區間上函數的單調性一致,∴函數f(x)在[1,2]上單調遞減,故B項正確;對于C,由B項的證明可知,y=f(x)圖象關于點(1,0)對稱,若f(x)的圖象同時關于直線 x=1對稱,則f(x)=0恒成立,這樣與“在區間[-1,0]上f(x)是增函數”矛盾,故C不正確;對于D,因為f(x)=f(1-(1-x))=-f(1+(1+x))=-f(x+2),所以f(x+2)=-f(x+4),可得f(x+4)=f(x),函數f(x)的周期是T=4,D項正確,故選C
考點:本題考查了函數的性質
點評:給出抽象函數,要我們在給出的幾條性質中找出錯誤的一項,著重考查了抽象函數的性質和函數單調性、奇偶性等知識,屬于中檔題


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com