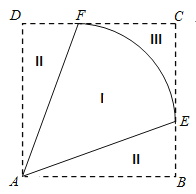
【題目】某地擬規(guī)劃種植一批芍藥，為了美觀，將種植區(qū)域（區(qū)域I）設計成半徑為1km的扇形
，中心角
（
）.為方便觀賞，增加收入，在種植區(qū)域外圍規(guī)劃觀賞區(qū)（區(qū)域II）和休閑區(qū)（區(qū)域III），并將外圍區(qū)域按如圖所示的方案擴建成正方形
，其中點
，
分別在邊
和
上．已知種植區(qū)、觀賞區(qū)和休閑區(qū)每平方千米的年收入分別是10萬元、20萬元、20萬元.
（1）要使觀賞區(qū)的年收入不低于5萬元，求
的最大值；
（2）試問：當為多少時，年總收入最大？
【答案】（1）
（2）
【解析】
（1）由
，
，
，所以
與
全等.
可得
，根據(jù)面積公式，可求得觀賞區(qū)的面積為
，要使得觀賞區(qū)的年收入不低于5萬元，則要求
，解不等式即可求出結果.
（2）由題意可得種植區(qū)的面積為
，正方形面積為
，設年總收入為
萬元，則
，利用導數(shù)在函數(shù)單調性中的應用，即可求出結果.
（1）∵，，，所以與全等.
所以，觀賞區(qū)的面積為
，要使得觀賞區(qū)的年收入不低于5萬元，則要求，即
，結合
可知
，則
的最大值為.
（2）種植區(qū)的面積為
，
正方形面積為
，
設年總收入為萬元，則
，
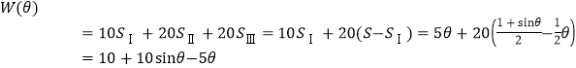其中，求導可得
.
當時，
，遞增；當
時，
，遞增.
所以當
時，取得最大值，此時年總收入最大.
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
、
，離心率
，點
在橢圓
上.
（1）求橢圓
的方程；
（2）設過點
且不與坐標軸垂直的直線交橢圓
于
、
兩點，線段
的垂直平分線與
軸交于點
，求點
的橫坐標的取值范圍；
（3）在第（2）問的條件下，求
面積的最大值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)
，曲線
在點
處的切線方程為
．
（1）求
，
的值；
（2）若
，求函數(shù)
的單調區(qū)間；
（3）設函數(shù)
，且
在區(qū)間
內存在單調遞減區(qū)間，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線
的焦點F（1，0），O為坐標原點，A，B是拋物線C上異于 O的兩點．
（1）求拋物線C的方程；
（2）若直線AB過點（8，0），求證：直線OA，OB的斜率之積為定值
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)
.
（1）若對定義域內的任意
，都有
成立，求實數(shù)
的值；
（2）若函數(shù)
的定義域上是單調函數(shù)，求實數(shù)
的取值范圍；
（3）若
，證明對任意的正整數(shù)
， 
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
經(jīng)過點
，且離心率為
．
（Ⅰ）求橢圓
的方程；
（Ⅱ）設
是橢圓上的點，直線
與
（
為坐標原點）的斜率之積為
．若動點
滿足
，試探究是否存在兩個定點
，使得
為定值？若存在，求的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
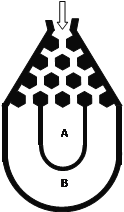
【題目】(本題滿分12分)將一個半徑適當?shù)男∏蚍湃肴鐖D所示的容器最上方的入口處,小球將自由下落.小球在下落過程中,將3次遇到黑色障礙物,最后落入
袋或
袋中.已知小球每次遇到黑色障礙物時向左、右兩邊下落的概率都是.
（Ⅰ）求小球落入袋中的概率
;
（Ⅱ）在容器入口處依次放入4個小球,記
為落入袋中小球的個數(shù),試求
的概率和的數(shù)學期望
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在四棱錐
中，
平面
，四邊形是菱形，
，
，
是
上任意一點。
（1）求證：
；
（2）當
面積的最小值是9時，在線段
上是否存在點
，使
與平面
所成角的正切值為2？若存在？求出
的值，若不存在，請說明理由
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
