
【題目】設(shè)函數(shù)![]() .
.
(1)若對定義域內(nèi)的任意![]() ,都有
,都有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的值;
的值;
(2)若函數(shù)![]() 的定義域上是單調(diào)函數(shù),求實數(shù)
的定義域上是單調(diào)函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,證明對任意的正整數(shù)
,證明對任意的正整數(shù)![]() ,
, ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】試題分析:(1)由![]() ,得
,得![]() 的定義域為
的定義域為![]() ,因為對
,因為對![]() ,都有
,都有![]() 成立,所以
成立,所以![]() 是函數(shù)
是函數(shù)![]() 的最小值,所以
的最小值,所以![]() ,即可求解
,即可求解![]() 的值;(2)由
的值;(2)由![]() ,函數(shù)
,函數(shù)![]() 在定義域上單調(diào)函數(shù),知
在定義域上單調(diào)函數(shù),知![]() 或
或![]() 在
在![]() 上恒成立,由此能求出實數(shù)
上恒成立,由此能求出實數(shù)![]() 的取值范圍;(3)當
的取值范圍;(3)當![]() 時,函數(shù)
時,函數(shù)![]() ,令
,令![]() ,
,
則![]() ,由此入手能夠證明
,由此入手能夠證明![]() .
.
試題解析:(1)由![]() ,得
,得![]() .∴
.∴![]() 的定義域為
的定義域為![]() .
.
因為對x∈![]() ,都有
,都有![]() ,∴
,∴![]() 是函數(shù)
是函數(shù)![]() 的最小值,故有
的最小值,故有![]() .
.
![]() 解得
解得![]() .
.
經(jīng)檢驗,![]() 時,
時,![]() 在
在![]() 上單調(diào)減,在
上單調(diào)減,在![]() 上單調(diào)增.
上單調(diào)增.![]() 為最小值.故得證.
為最小值.故得證.
(2)∵![]() 又函數(shù)
又函數(shù)![]() 在定義域上是單調(diào)函數(shù),
在定義域上是單調(diào)函數(shù),
∴![]() 或
或![]() 在
在![]() 上恒成立.
上恒成立.
若![]() ,則
,則![]() 在
在![]() 上恒成立,
上恒成立,
即![]() =
=![]() 恒成立,由此得
恒成立,由此得![]()
![]() ;
;
若![]() ,則
,則![]() 在
在![]() 上恒成立,
上恒成立,
即![]() =
=![]() 恒成立.
恒成立.
因![]() 在
在![]() 上沒有最小值,∴不存在實數(shù)
上沒有最小值,∴不存在實數(shù)![]() 使
使![]() 恒成立.
恒成立.
綜上所述,實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.
(3)當![]() 時,函數(shù)
時,函數(shù)![]() .
.
令![]() ,
,
則![]() .
.
當![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)遞減.
上單調(diào)遞減.
又![]() ,
,![]() 當
當![]() 時,恒有
時,恒有![]() ,即
,即![]() 恒成立.
恒成立.
故當![]() 時,有
時,有![]() .
.
而![]() ,
,![]() .取
.取![]() ,則有
,則有![]() .
.
![]()
![]() .所以結(jié)論成立.
.所以結(jié)論成立.


科目:高中數(shù)學 來源: 題型:
【題目】我國古代數(shù)學名著《續(xù)古摘奇算法》(楊輝)一書中有關(guān)于三階幻方的問題:將1,2,3,4,5,6,7,8,9分別填入![]() 的方格中,使得每一行,每一列及對角線上的三個數(shù)的和都相等(如圖所示),我們規(guī)定:只要兩個幻方的對應位置(如每行第一列的方格)中的數(shù)字不全相同,就稱為不同的幻方,那么所有不同的三階幻方的個數(shù)是( )
的方格中,使得每一行,每一列及對角線上的三個數(shù)的和都相等(如圖所示),我們規(guī)定:只要兩個幻方的對應位置(如每行第一列的方格)中的數(shù)字不全相同,就稱為不同的幻方,那么所有不同的三階幻方的個數(shù)是( )
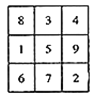
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】將集合M={1,2,3,...,15}表示為它的5個三元子集(三元集:含三個元素的集合)的并集,并且這些三元子集的元素之和都相等,則每個三元集的元素之和為________;請寫出滿足上述條件的集合M的5個三元子集__________(只寫出一組)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】圍建一個面積為360![]() 的矩形場地,要求矩形場地的一面利用舊墻(利用舊墻需維修),其它三面圍墻要新建,在舊墻的對面的新墻上要留一個寬度為2m的進出口,如圖所示,已知舊墻的維修費用為45元/m,新墻的造價為180元/m,設(shè)利用的舊墻的長度為
的矩形場地,要求矩形場地的一面利用舊墻(利用舊墻需維修),其它三面圍墻要新建,在舊墻的對面的新墻上要留一個寬度為2m的進出口,如圖所示,已知舊墻的維修費用為45元/m,新墻的造價為180元/m,設(shè)利用的舊墻的長度為![]() (單位:
(單位:![]() ),修建此矩形場地圍墻的總費用為
),修建此矩形場地圍墻的總費用為![]() (單位:元)
(單位:元)
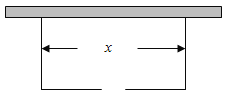
(1)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(2)試確定![]() ,使修建此矩形場地圍墻的總費用最小,并求出最小總費用。
,使修建此矩形場地圍墻的總費用最小,并求出最小總費用。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(1)若曲線![]() 的一條切線經(jīng)過點
的一條切線經(jīng)過點![]() ,求這條切線的方程.
,求這條切線的方程.
(2)若關(guān)于![]() 的方程
的方程![]() 有兩個不相等的實數(shù)根x1,x2。
有兩個不相等的實數(shù)根x1,x2。
①求實數(shù)a的取值范圍;
②證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,四棱錐P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD, ![]() ,M為PC的中點,N點在AB上且
,M為PC的中點,N點在AB上且![]() .
.
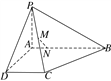
(1)證明:MN∥平面PAD;
(2)求直線MN與平面PCB所成的角.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com