分析:(1)連接A
1C
1、AC和BD交于O,連接C
1O.證明BD垂直平面平面AC
1內的兩條相交直線AC,C
1O,即可證明C
1C⊥BD;
(2)當
=1時,能使A
1C⊥平面C
1BD,A
1C與C
1O相交于G,說明點G是正三角形C
1BD的中心,證明CG⊥平面C
1BD,即可證明A
1C⊥平面C
1BD.
解答:(1)證明:如圖,連接A
1C
1、AC和BD交于O,連接C
1O.
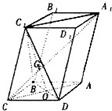
∵四邊形ABCD是菱形,
∴AC⊥BD,BC=CD.
又∵∠BCC
1=∠DCC
1,C
1C=C
1C,
∴△C
1BC≌△C
1DC,
∴C
1B=C
1D,
∵DO=OB
∴C
1O⊥BD,(3分)
但AC⊥BD,AC∩C
1O=O,
∴BD⊥平面AC
1,
又C
1C?平面AC
1,
∴C
1C⊥BD.(6分)
(2)當
=1時,能使A
1C⊥平面C
1BD.
∵
=1,
∴BC=CD=C
1C,
又∠BCD=∠C
1CB=∠C
1CD,
由此可推得BD=C
1B=C
1D.
∴三棱錐C-C
1BD是正三棱錐.(9分)
設A
1C與C
1O相交于G.
∵A
1C
1∥AC,且A
1C
1:OC=2:1,
∴C
1G:GO=2:1.
又C
1O是正三角形C
1BD的BD邊上的高和中線,
∴點G是正三角形C
1BD的中心,
∴CG⊥平面C
1BD,
即A
1C⊥平面C
1BD.(12分)
點評:本小題主要考查直線與直線、直線與平面的關系,邏輯推理能力,考查空間想象能力,是中檔題.

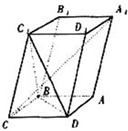 如圖,已知平行六面體ABCD-A1B1C1D1的底面ABCD上菱形,且∠C1CB=∠C1CD=∠BCD,
如圖,已知平行六面體ABCD-A1B1C1D1的底面ABCD上菱形,且∠C1CB=∠C1CD=∠BCD,


 如圖,已知平行六面體OABC-O1A1B1C1,點G是上底面O1A1B1C1的中心,且
如圖,已知平行六面體OABC-O1A1B1C1,點G是上底面O1A1B1C1的中心,且 如圖,已知平行六面體ABC-A1B1C1的底面為正方形,O1,O分別為上、下底面中心,且A1在底面ABCD上的射影為O.
如圖,已知平行六面體ABC-A1B1C1的底面為正方形,O1,O分別為上、下底面中心,且A1在底面ABCD上的射影為O. 如圖,已知平行六面體ABCD-A1B1C1D1的底面為正方形,O1,O分別為上、下底面中心,且A1在底面ABCD上的射影為O.
如圖,已知平行六面體ABCD-A1B1C1D1的底面為正方形,O1,O分別為上、下底面中心,且A1在底面ABCD上的射影為O. 如圖,已知平行六面體ABCD-A1B1C1D1(底面是平行四邊形的四棱柱)
如圖,已知平行六面體ABCD-A1B1C1D1(底面是平行四邊形的四棱柱) 如圖,已知平行六面體ABCD-A1B1C1D1的底面為正方形,O1,O分別為上、下底面的中心,且A1在底面ABCD上的射影是O.
如圖,已知平行六面體ABCD-A1B1C1D1的底面為正方形,O1,O分別為上、下底面的中心,且A1在底面ABCD上的射影是O.