
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為矩形,平面PCD⊥平面ABCD,AB=2,BC=1,![]() ,E為PB中點.
,E為PB中點.
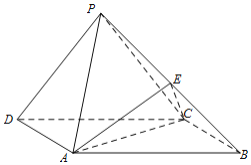
(Ⅰ)求證:PD∥平面ACE;
(Ⅱ)求證:PD⊥平面PBC;
(Ⅲ)求三棱錐E-ABC的體積.
【答案】(I)見解析;(II)見解析;(III)![]()
【解析】
(I)連結(jié)![]() 交
交![]() 于
于![]() ,連結(jié)
,連結(jié)![]() ,利用中位線可證明
,利用中位線可證明![]() ,即可說明
,即可說明![]() 平面
平面![]() ;
;
(II)由平面![]() 平面
平面![]() ,底面
,底面![]() 為矩形可得:
為矩形可得:![]() ,根據(jù)勾股定理可得:
,根據(jù)勾股定理可得:![]() ,由此證明
,由此證明![]() 平面
平面![]() ;
;
(III)取![]() 的中點
的中點![]() ,連結(jié)
,連結(jié)![]() ,可證明
,可證明![]() 平面
平面![]() ,由于
,由于![]() 為
為![]() 中點,則過
中點,則過![]() 點作平面
點作平面![]() 的高等于
的高等于![]() ,所以
,所以![]() ,即可求出三棱錐
,即可求出三棱錐![]() 的體積
的體積
(I)連結(jié)![]() 交
交![]() 于
于![]() ,連結(jié)
,連結(jié)![]() .因為底面
.因為底面![]() 是矩形,
是矩形,
所以![]() 為
為![]() 中點.又因為
中點.又因為![]() 為
為![]() 中點,所以
中點,所以![]() .因為
.因為![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(II) 因為底面![]() 為矩形,所以
為矩形,所以![]() .
.
又因為平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .因為
.因為![]() 平面
平面![]() ,所以
,所以![]() .
.
因為![]() ,所以
,所以![]() ,即
,即![]() .
.
因為![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(III))取![]() 的中點
的中點![]() ,連結(jié)
,連結(jié)![]() ,因為
,因為![]() ,
,![]() 是
是![]() 的中點,所以
的中點,所以![]() ,且
,且![]() ,
,
因為平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() , 所以
, 所以![]() 平面
平面![]() ,因為
,因為![]() 為
為![]() 中點,
中點,
所以![]() .
.
所以三棱錐![]() C的體積為
C的體積為![]() .
.


科目:高中數(shù)學 來源: 題型:
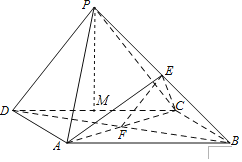
【題目】如圖,在三棱錐![]() 中,底面為正三角形,側(cè)棱垂直于底面,
中,底面為正三角形,側(cè)棱垂直于底面,![]() .若
.若![]() 是棱
是棱![]() 上的點,且
上的點,且![]() ,則異面直線
,則異面直線![]() 與
與![]() 所成角的余弦值為( )
所成角的余弦值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知四棱錐![]() 的底面為直角梯形,
的底面為直角梯形,![]() ,
,![]() ,
,![]() 底面
底面![]() ,且
,且![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.

(1)證明:面![]() 面
面![]() ;
;
(2)求![]() 與
與![]() 夾角的余弦值;
夾角的余弦值;
(3)求面![]() 與面
與面![]() 所成二面角余弦值的大小.
所成二面角余弦值的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 的前n項和
的前n項和![]() ,
, ![]() 是等差數(shù)列,且
是等差數(shù)列,且![]() .
.
(Ⅰ)求數(shù)列![]() 的通項公式;
的通項公式;
(Ⅱ)令 .求數(shù)列
.求數(shù)列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
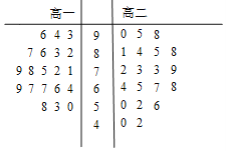
【題目】某學校為了解學生的體質(zhì)健康狀況,對高一、高二兩個年級的學生進行了體質(zhì)測試.現(xiàn)從兩個年級學生中各隨機選取20人,將他們的測試數(shù)據(jù),用莖葉圖表示如圖:《國家學生體質(zhì)健康標準》的等級標準如表.規(guī)定:測試數(shù)據(jù)≥60,體質(zhì)健康為合格.
等級 | 優(yōu)秀 | 良好 | 及格 | 不及格 |
測試數(shù)據(jù) |
|
|
|
|
(Ⅰ)從該校高二年級學生中隨機選取一名學生,試估計這名學生體質(zhì)健康合格的概率;
(Ⅱ)從兩個年級等級為優(yōu)秀的樣本中各隨機選取一名學生,求選取的兩名學生的測試數(shù)據(jù)平均數(shù)大于95的概率;
(Ⅲ)設(shè)該校高一學生測試數(shù)據(jù)的平均數(shù)和方差分別為![]() ,高二學生測試數(shù)據(jù)的平均數(shù)和方差分別為
,高二學生測試數(shù)據(jù)的平均數(shù)和方差分別為![]() ,試估計
,試估計![]() 、
、![]() 的大小.(只需寫出結(jié)論)
的大小.(只需寫出結(jié)論)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某餐廳通過查閱了最近5次食品交易會參會人數(shù)![]() (萬人)與餐廳所用原材料數(shù)量
(萬人)與餐廳所用原材料數(shù)量![]() (袋),得到如下統(tǒng)計表:
(袋),得到如下統(tǒng)計表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
參會人數(shù) | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根據(jù)所給5組數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() .
.
(2)已知購買原材料的費用![]() (元)與數(shù)量
(元)與數(shù)量![]() (袋)的關(guān)系為
(袋)的關(guān)系為![]() ,
,
投入使用的每袋原材料相應(yīng)的銷售收入為700元,多余的原材料只能無償返還,據(jù)悉本次交易大會大約有15萬人參加,根據(jù)(1)中求出的線性回歸方程,預測餐廳應(yīng)購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤![]() 銷售收入
銷售收入![]() 原材料費用).
原材料費用).
參考公式:  ,
, ![]() .
.
參考數(shù)據(jù): ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點![]() 是橢圓
是橢圓![]() 的一個頂點,且橢圓N的離心率為
的一個頂點,且橢圓N的離心率為![]() .
.
(1)求橢圓N的方程;
(2)已知![]() 是橢圓N的左焦點,過
是橢圓N的左焦點,過![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,
,![]() 交橢圓N于
交橢圓N于![]() 兩點,
兩點,![]() 交橢圓N于
交橢圓N于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上的最小值為
上的最小值為![]() ,若不等式
,若不等式![]() 有解,求實數(shù)
有解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學校為調(diào)查高三年級學生的身高情況,按隨機抽樣的方法抽取80名學生,得到男生身高情況的頻率分布直方圖(如圖(1))和女生身高情況的頻率分布直方圖(如圖(2)).已知圖(1)中身高在170~175cm的男生有16名.
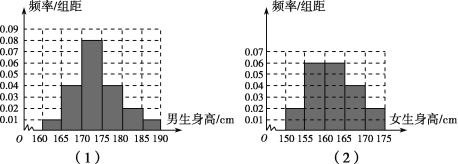
(1)試問在抽取的學生中,男、女生各有多少名?
身高≥170cm | 身高<170cm | 總計 | |
男生 | |||
女生 | |||
總計 |
(2)根據(jù)頻率分布直方圖,完成下面的2×2列聯(lián)表,并判斷能有多大(百分數(shù))的把握認為身高與性別有關(guān)?
附:參考公式和臨界值表
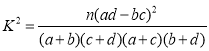
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com