
 ,數列{an}滿足
,數列{an}滿足 .
. ,這些項能夠構成以a1為首項,q(0<q<5,q∈N*)為公比的等比數列
,這些項能夠構成以a1為首項,q(0<q<5,q∈N*)為公比的等比數列 ,k∈N*.若存在,寫出nk關于k的表達式;若不存在,說明理由.
,k∈N*.若存在,寫出nk關于k的表達式;若不存在,說明理由.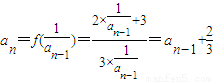 ,(n∈N*,且n≥2),
,(n∈N*,且n≥2),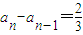 .由此可知
.由此可知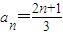 .
.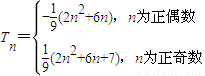 ,由此計算能導出實數t的取值范圍.
,由此計算能導出實數t的取值范圍.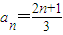 ,知數列{an}中每一項都不可能是偶數.存在以a1為首項,公比q為2或4的數列
,知數列{an}中每一項都不可能是偶數.存在以a1為首項,公比q為2或4的數列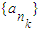 ,k∈N*,
,k∈N*,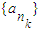 ,中每一項除第一項外都是偶數,故不存在以a1為首項,公比為偶數的數列
,中每一項除第一項外都是偶數,故不存在以a1為首項,公比為偶數的數列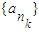 ,.再由q=1和q=3分別討論知存在滿足條件的數列{ank},且
,.再由q=1和q=3分別討論知存在滿足條件的數列{ank},且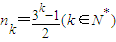 .
. ,(n∈N*,且n≥2),
,(n∈N*,且n≥2),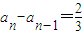 .(2分)
.(2分) 的等差數列.
的等差數列.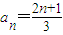 .(4分)
.(4分)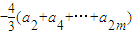
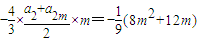 =
=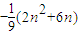 .(6分)
.(6分)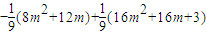 =
=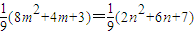 .(8分)
.(8分)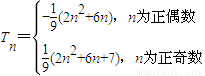
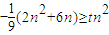 ,(n為正偶數)恒成立.
,(n為正偶數)恒成立.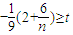 ,對n為正偶數恒成立,
,對n為正偶數恒成立,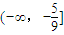 .(10分)
.(10分)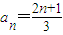 ,知數列{an}中每一項都不可能是偶數.
,知數列{an}中每一項都不可能是偶數.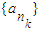 ,k∈N*,
,k∈N*,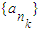 中每一項除第一項外都是偶數,故不存在以a1為首項,公比為偶數的數列
中每一項除第一項外都是偶數,故不存在以a1為首項,公比為偶數的數列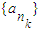 .(12分)
.(12分)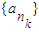 .
.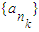 ,k∈N*.
,k∈N*.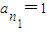 ,n1=1,
,n1=1,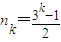 .
.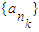 ,且
,且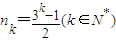 .(14分)
.(14分)

科目:高中數學 來源:2009-2010學年廣東省湛江市遂溪一中高三(下)4月月考數學試卷(理科)(解析版) 題型:解答題
 ,數列{an}滿足
,數列{an}滿足
 ,試比較 Sn與
,試比較 Sn與 的大小,并加以證明.
的大小,并加以證明.查看答案和解析>>
科目:高中數學 來源:2009-2010學年廣東省湛江市遂溪一中高三(下)4月月考數學試卷(文科)(解析版) 題型:解答題
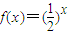 ,數列{an} 滿足
,數列{an} 滿足 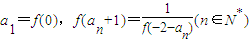
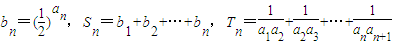 ,求 Sn與 Tn.
,求 Sn與 Tn.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com