
【題目】如圖,多面體![]() 中,四邊形
中,四邊形![]() 是
是![]() 為鈍角的平行四邊形,四邊形
為鈍角的平行四邊形,四邊形![]() 為直角梯形,
為直角梯形,![]() 且
且![]() .
.
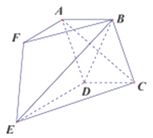
(1)求證:![]() ;
;
(2)若點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)利用勾股定理證得![]() ,結合
,結合![]() ,證得
,證得![]() 平面
平面![]() ,根據線線平行證得
,根據線線平行證得![]() 平面
平面![]() ,由此證得
,由此證得![]() .判斷出四邊形
.判斷出四邊形![]() 為菱形,由此證得
為菱形,由此證得![]() ,由此證得
,由此證得![]() 平面
平面![]() ,從而證得
,從而證得![]() .
.
(2)利用第一問的結論,判斷出線![]() 與平面
與平面![]() 所成角,結合點
所成角,結合點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,求得
,求得![]() 的長,然后通過解三角形,把相應的線面角的正弦值求出.
的長,然后通過解三角形,把相應的線面角的正弦值求出.
(1)在![]() 中,
中,![]() ,所以
,所以![]()
又因為![]() ,所以
,所以![]() 平面
平面![]() ,因為
,因為![]()
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
在平行四邊形![]() 中,且
中,且![]() ,所以平行四邊形
,所以平行四邊形![]() 為菱形
為菱形
于是![]()
所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() .
.
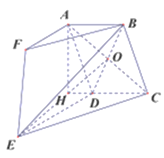
(2)因為![]() 平面
平面![]() 且垂足為
且垂足為![]() ,所以
,所以![]() 為直線
為直線![]() 與平面
與平面![]() 所成角.
所成角.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所
,所![]() ,
,
所以![]() 到平面
到平面![]() 的距離為
的距離為![]() 到平面
到平面![]() 的距離.
的距離.![]()
所以![]() 平面
平面![]() 平面
平面![]()
所以平面![]() 平面
平面![]() 且交線為
且交線為![]()
過![]() 作
作![]() ,則
,則![]() ,所以
,所以![]()
所以![]() ,所以
,所以![]()
在![]() 中,
中,![]() ,
,
所以![]() .所以直線
.所以直線![]() 與平面
與平面![]() 所成角的正弦值
所成角的正弦值![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為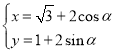 (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() ,(t為參數),在以原點為極點,x軸正半軸為極軸的極坐標中,曲線
,(t為參數),在以原點為極點,x軸正半軸為極軸的極坐標中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)將![]() 與
與![]() 的方程化為極坐標方程;
的方程化為極坐標方程;
(2)若曲線![]() 與
與![]() 的公共點都在
的公共點都在![]() 上,
上,![]() ,求r.
,求r.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016里約奧運會期間,小趙常看的4個電視頻道中有2個頻道在轉播奧運比賽,若小趙這時打開電視,隨機打開其中兩個頻道試看,那么,小趙所看到的第一個電視臺恰好沒有轉播奧運比賽,而第二個電視臺恰好在轉播奧運比賽的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲線y=f(x)上總存在兩點M(x1,y1),N(x2,y2),使曲線y=f(x)在M,N兩點處的切線互相平行,則x1+x2的取值范圍為
,k∈[4,+∞),曲線y=f(x)上總存在兩點M(x1,y1),N(x2,y2),使曲線y=f(x)在M,N兩點處的切線互相平行,則x1+x2的取值范圍為
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以該直角坐標系的原點
為參數),以該直角坐標系的原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,交曲線
兩點,交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com