
【題目】如圖,AB為⊙O的直徑,點E在⊙O上,C為 ![]() 的中點,過點C作直線CD⊥AE于D,連接AC、BC.
的中點,過點C作直線CD⊥AE于D,連接AC、BC.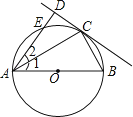
(1)試判斷直線CD與⊙O的位置關系,并說明理由;
(2)若AD=2,AC= ![]() ,求AB的長.
,求AB的長.
【答案】
(1)
解:相切,連接OC,
∵C為 ![]() 的中點,
的中點,
∴∠1=∠2,
∵OA=OC,
∴∠1=∠ACO,
∴∠2=∠ACO,
∴AD∥OC,
∵CD⊥AD,
∴OC⊥CD,
∴直線CD與⊙O相切;
(2)
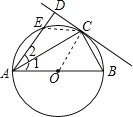
解:方法1:連接CE,
∵AD=2,AC= ![]() ,
,
∵∠ADC=90°,
∴CD= ![]() =
= ![]() ,
,
∵CD是⊙O的切線,
∴CD2=ADDE,
∴DE=1,
∴CE= ![]() =
= ![]() ,
,
∵C為 ![]() 的中點,
的中點,
∴BC=CE= ![]() ,
,
∵AB為⊙O的直徑,
∴∠ACB=90°,
∴AB= ![]() =3.
=3.
方法2:∵∠DCA=∠B,
易得△ADC∽△ACB,
∴ ![]() =
= ![]() ,
,
∴AB=3.
【解析】本題考查了直線與圓的位置關系,切線的判定和性質,圓周角定理,勾股定理,平行線的性質,切割線定理,熟練掌握各定理是解題的關鍵.(1)連接OC,由C為 ![]() 的中點,得到∠1=∠2,等量代換得到∠2=∠ACO,根據平行線的性質得到OC⊥CD,即可得到結論;
的中點,得到∠1=∠2,等量代換得到∠2=∠ACO,根據平行線的性質得到OC⊥CD,即可得到結論;
(2)連接CE,由勾股定理得到CD= ![]() =
= ![]() ,根據切割線定理得到CD2=ADDE,根據勾股定理得到CE=
,根據切割線定理得到CD2=ADDE,根據勾股定理得到CE= ![]() =
= ![]() ,由圓周角定理得到∠ACB=90°,即可得到結論.
,由圓周角定理得到∠ACB=90°,即可得到結論.
【考點精析】通過靈活運用直線與圓的三種位置關系,掌握直線與圓有三種位置關系:無公共點為相離;有兩個公共點為相交,這條直線叫做圓的割線;圓與直線有唯一公共點為相切,這條直線叫做圓的切線,這個唯一的公共點叫做切點即可以解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,正方體![]() 的棱長為
的棱長為![]() ,
,![]() ,
,![]() 分別是棱
分別是棱![]() ,
,![]() 的中點,過直線
的中點,過直線![]() ,
,![]() 的平面分別與棱
的平面分別與棱![]() 、
、![]() 交于
交于![]() ,
,![]() ,設
,設![]() ,
,![]() ,給出以下四個命題:
,給出以下四個命題:
①平面![]() 平面
平面![]() ;
;
②當且僅當![]() 時,四邊形
時,四邊形![]() 的面積最小;
的面積最小;
③四邊形![]() 周長
周長![]() ,
,![]() 是單調函數;
是單調函數;
④四棱錐![]() 的體積
的體積![]() 為常函數;
為常函數;
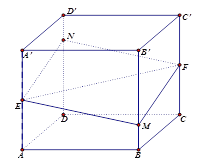
以上命題中假命題的序號為( ).
A. ①④ B. ② C. ③ D. ③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家規定,中小學生每天在校體育活動時間不低于1小時,為了解這項政策的落實情況,有關部門就“你某天在校體育活動時間是多少”的問題,在某校隨機抽查了部分學生,再根據活動時間t(小時)進行分組(A組:t<0.5,B組:0.5≤t≤1,C組:1≤t<1.5,D組:t≥1.5),繪制成如下兩幅不完整統計圖,請根據圖中信息回答問題:
(1)此次抽查的學生數為人;
(2)補全條形統計圖;
(3)從抽查的學生中隨機詢問一名學生,該生當天在校體育活動時間低于1小時的概率是
(4)若當天在校學生數為1200人,請估計在當天達到國家規定體育活動時間的學生有人.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2016年龍巖市初中體育中考中,隨意抽取某校5位同學一分鐘跳繩的次數分別為:158,160,154,158,170,則由這組數據得到的結論錯誤的是( )
A.平均數為160
B.中位數為158
C.眾數為158
D.方差為20.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在生產過程中,測得纖維產品的纖度(表示纖維粗細的一種量)共有100個數據,將數據分組如表:
分組 | 頻數 |
|
|
|
|
|
|
|
|
|
|
|
|
合計 |
|
(1)畫出頻率分布表,并畫出頻率分布直方圖;
(2)估計纖度落在![]() 中的概率及纖度小于
中的概率及纖度小于![]() 的概率是多少?
的概率是多少?
(3)從頻率分布直方圖估計出纖度的眾數、中位數和平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1是某公交公司1路車從起點站A站途經B站和C站,最終到達終點站D站的格點站路線圖.(8×8的格點圖是由邊長為1的小正方形組成)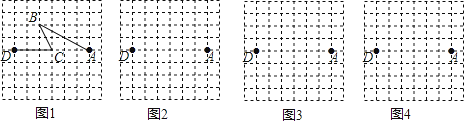
(1)求1路車從A站到D站所走的路程(精確到0.1);
(2)在圖2、圖3和圖4的網格中各畫出一種從A站到D站的路線圖.(要求:①與圖1路線不同、路程相同;②途中必須經過兩個格點站;③所畫路線圖不重復)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高科技企業生產產品A和產品B需要甲、乙兩種新型材料.生產一件產品A需要甲材料1.5kg,乙材料1kg,用5個工時;生產一件產品B需要甲材料0.5kg,乙材料0.3kg,用3個工時.生產一件產品A的利潤為2100元,生產一件產品B的利潤為900元.該企業現有甲材料150kg,乙材料90kg,求在不超過600個工時的條件下,生產產品A和產品B的利潤之和的最大值(元).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com