
【題目】
如圖,在直三棱柱![]() 中,平面
中,平面![]() 側面A1ABB1.
側面A1ABB1.
(Ⅰ)求證:![]() ;
;
(Ⅱ)若直線AC與平面A1BC所成的角為θ,二面角A1-BC-A的大小為φ,試判斷θ與φ的大小關系,并予以證明.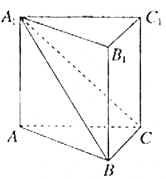
【答案】(Ⅰ)證明見解析.
(Ⅱ)![]() ,證明見解析.
,證明見解析.
【解析】
(Ⅰ)證明:如右圖,過點A在平面A1ABB1內作AD⊥A1B于D,則
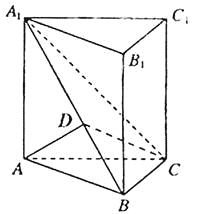
由平面A1BC⊥側面A1ABB1,且平面A1BC![]() 側面A1ABB1=A1B,得
側面A1ABB1=A1B,得
AD⊥平面A1BC,又BC![]() 平面A1BC,所以AD⊥BC.
平面A1BC,所以AD⊥BC.
因為三棱柱ABC—A1B1C1是直三棱柱,則AA1⊥底面ABC,所以AA1⊥BC.
又AA1![]() AD=A,從而BC⊥側面A1ABB1,
AD=A,從而BC⊥側面A1ABB1,
又AB![]() 側面A1ABB1,故AB⊥BC.
側面A1ABB1,故AB⊥BC.
(Ⅱ)解法1:連接CD,則由(Ⅰ)知![]() 是直線AC與平面A1BC所成的角,
是直線AC與平面A1BC所成的角,
![]() 是二面角A1—BC—A的平面角,即
是二面角A1—BC—A的平面角,即![]()
于是在![]() 中,
中,![]() 在
在![]() 中,
中,![]() ,
,
由![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() .
.
解法2:由(1)知,以點![]() 為坐標原點,以
為坐標原點,以![]() 、
、![]() 、
、![]() 所在的直線分
所在的直線分![]() 軸、
軸、![]() 軸、
軸、![]() 軸,建立如圖所示的空間直角坐標系,
軸,建立如圖所示的空間直角坐標系,

設![]() ,
,
則![]() ,
,
于是![]() ,
,![]() .
.
設平面的一個法向量為![]() ,則
,則
由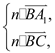 得
得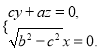
可取![]() ,于是
,于是![]() 與
與![]() 的夾角
的夾角![]() 為銳角,則
為銳角,則![]() 與
與![]() 互為余角.
互為余角.
所以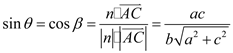 ,
,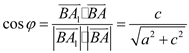 ,
,
所以![]() .
.
于是由![]() ,得
,得![]() ,
,
即![]() ,又
,又![]() 所以
所以![]() .
.
第(1)問證明線線垂直,一般先證線面垂直,再由線面垂直得線線垂直;第(2)問若用傳統方法一般來說要先作垂直,進而得直角三角形.若用向量方法,關鍵在求法向量.


科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左焦點為
的左焦點為![]() ,下頂點為
,下頂點為![]() ,上頂點為
,上頂點為![]() ,
,![]() 是等邊三角形.
是等邊三角形.
(Ⅰ)求橢圓的離心率;
(Ⅱ)設直線![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線與橢圓交于點
的直線與橢圓交于點![]()
![]() 異于點
異于點![]() ,線段
,線段![]() 的垂直平分線與直線
的垂直平分線與直線![]() 交于點
交于點![]() ,與直線
,與直線![]() 交于點
交于點![]() ,若
,若![]() .
.
(ⅰ)求![]() 的值;
的值;
(ⅱ)已知點![]() ,點
,點![]() 在橢圓上,若四邊形
在橢圓上,若四邊形![]() 為平行四邊形,求橢圓的方程.
為平行四邊形,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,且
,且![]() 在橢圓
在橢圓![]() 上運動,當點
上運動,當點![]() 恰好在直線l:
恰好在直線l:![]() 上時,
上時,![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)作與![]() 平行的直線
平行的直線![]() ,與橢圓交于
,與橢圓交于![]() 兩點,且線段
兩點,且線段![]() 的中點為
的中點為![]() ,若
,若![]() 的斜率分別為
的斜率分別為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,函數
,函數![]() 在
在![]() ,
,![]() 處取得極值,其中
處取得極值,其中![]() .
.
(1)求實數t的取值范圍;
(2)判斷![]() 在
在![]() 上的單調性并證明;
上的單調性并證明;
(3)已知![]() 在
在![]() 上的任意
上的任意![]() 、
、![]() ,都有
,都有![]() ,令
,令![]() ,若函數
,若函數![]() 有3個不同的零點,求實數m的取值范圍.
有3個不同的零點,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2010-2018年之間,受益于基礎設施建設對光纖產品的需求,以及個人計算機及智能手機的下一代規格升級,電動汽車及物聯網等新機遇,連接器行業增長呈現加速狀態.根據該折線圖,下列結論正確的個數為( )

①每年市場規模量逐年增加;
②增長最快的一年為2013~2014;
③這8年的增長率約為40%;
④2014年至2018年每年的市場規模相對于2010年至2014年每年的市場規模,數據方差更小,變化比較平穩
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人準備投資1200萬元辦一所中學,為了考慮社會效益和經濟效益,對該地區教育市場進行調查,得出一組數據,列表如下(以班級為單位).
市場調查表:
班級學生數 | 配備教師數 | 硬件建設費(萬元) | 教師年薪(萬元) | |
初中 | 50 | 2.0 | 28 | 1.2 |
高中 | 40 | 2.5 | 58 | 1.6 |
根據物價部門的有關規定:初中是義務教育階段,收費標準適當控制,預計除書本費、辦公費外,初中每人每年可收取600元.高中每人每年可收取1500元.因生源和環境等條件限制,辦學規模以20至30個班為宜(含20個班與30個),教師實行聘任制.初、高中教育周期均為三年,設初中編制為![]() 個班,高中編制為
個班,高中編制為![]() 個班,請你合理地安排招生計劃,使年利潤最大.
個班,請你合理地安排招生計劃,使年利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 1(a>b>0)的左右焦點分別為F1F2,左右頂點分別為AB,上頂點為T,且△TF1F2為等邊三角形.
1(a>b>0)的左右焦點分別為F1F2,左右頂點分別為AB,上頂點為T,且△TF1F2為等邊三角形.
(1)求此橢圓的離心率e;
(2)若直線y=kx+m(k>0)與橢圓交與CD兩點(點D在x軸上方),且與線段F1F2及橢圓短軸分別交于點MN(其中MN不重合),且|CM|=|DN|.
①求k的值;
②設ADBC的斜率分別為k1,k2,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com